Which Real Root is Larger: x^8 = 8 - 10x^9 or x^10 = 8 - 10x^11?

[anemone]

Which is larger, the real root of x + x² + ... + x⁸ = 8 - 10x⁹, or the real root of x + x² + ... + x¹⁰ = 8 - 10x¹¹?

 

[HallsofIvy]

The second one. The first has root about 0.882, the second, bout 0.884. I got that by graphing both and then "zooming" in on the zeros.

 

[Mathwebster]

Here's my solution

Spoiler

It's not hard to show that the derivative of each is positive so both are increasing function meaning there's only one root. Let

$f(x) = 1 + x + x^2+ \cdots +x^8 + 10x^9 - 8$

and

$g(x) = 1 + x + x^2+ \cdots + x^{10} + 10x^{11} - 8$

We also have $f(0.8) <0, \; f(0.9) >0, \;g(0.8) <0, \;g(0.9) >0$ meaning that both roots lie between $0.8$ and $0.9$. Now consider the difference $h(x) = f(x)-g(x) =9x^8-x^{10}-10x^{11}= -(x+1)(10x-9)x^9 $. On the interval $(0.8,0.9)$ $h(x)> 0$ meaning that $ f(x) > g(x)$ giving that the root of $g(x)$ is larger than the root of $f(x)$ as HallsofIvy pointed out.

 

[anemone]

The second one. The first has root about 0.882, the second, bout 0.884. I got that by graphing both and then "zooming" in on the zeros.

Here's my solution

Spoiler

It's not hard to show that the derivative of each is positive so both are increasing function meaning there's only one root. Let

$f(x) = 1 + x + x^2+ \cdots +x^8 + 10x^9 - 8$

and

$g(x) = 1 + x + x^2+ \cdots + x^{10} + 10x^{11} - 8$

We also have $f(0.8) <0, \; f(0.9) >0, \;g(0.8) <0, \;g(0.9) >0$ meaning that both roots lie between $0.8$ and $0.9$. Now consider the difference $h(x) = f(x)-g(x) =9x^8-x^{10}-10x^{11}= -(x+1)(10x-9)x^9 $. On the interval $(0.8,0.9)$ $h(x)> 0$ meaning that $ f(x) > g(x)$ giving that the root of $g(x)$ is larger than the root of $f(x)$ as HallsofIvy pointed out.

Thanks for participating to both of you!:)

Hi Jester, it took me a fraction of time to decipher why $h(x)> 0$ on the interval $(0.8,0.9) in your approach! Well done!

I want to also let you know that my method is so much different than you and... it's less elegant but it works!

 

[anemone]

Which is larger, the real root of x + x² + ... + x⁸ = 8 - 10x⁹, or the real root of x + x² + ... + x¹⁰ = 8 - 10x¹¹?

My solution:

Spoiler

First, notice that

[TABLE="class: grid, width: 500"]
[TR]
[TD]$1-x^9=(1-x)(x+x^2+\cdots+x^8)$

$1-x^9=(1-x)(8-10x^9)$

$1-x^9=8-10x^9-8x+10x^{10}$

$10x^{10}-9x^9-8x+7=0$[/TD]
[TD]$1-x^{11}=(1-x)(x+x^2+\cdots+x^{10})$

$1-x^{11}=(1-x)(8-10x^{11})$

$1-x^{11}=8-10x^{11}-8x+10x^{12}$

$10x^{12}-9x^{11}-8x+7=0$[/TD]
[/TR]
[TR]
[TD]So I let

$f(x)=10x^{10}-9x^9-8x+7$[/TD]
[TD]So I let

$g(x)=10x^{12}-9x^{11}-8x+7$[/TD]
[/TR]
[TR]
[TD]Descartes's Rule says $f(x)$ has two positive real roots and obviously $x=1$ is one of the root of $f(x)$ and the other root lies between $(0, 1)$.[/TD]
[TD]Descartes's Rule says $g(x)$ has two positive real roots and obviously $x=1$ is one of the root of $g(x)$ and the other root lies between $(0, 1)$.[/TD]
[/TR]
[/TABLE]

Observe also that

$g(x)=10x^{12}-9x^{11}-8x+7=x^2(10x^{10}-9x^9-8x+7)-8x+7+8x^3-7x^2=x^2f(x)+(8x-7)(x^2-1)$

If $a$ is a root of the function of $f$, then

$g(a)=a^2f(a)+(8a-7)(a^2-1)$

$g(a)=0+(8a-7)(a^2-1)$

$g(a)=(8a-7)(a^2-1)$

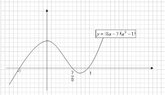
And here is a rough sketch of the graph $y=(8a-7)(a^2-1)$

View attachment 1544

So, if $\dfrac{7}{8}<a<1$, then $g(a)<0$ whereas if $a<\dfrac{7}{8}$, then $g(a)>0$.

Now, our objective is to find out whether the root of the function of $f$ is greater than or less than $\dfrac{7}{8}$.

$f(\dfrac{7}{8})=10(\dfrac{7}{8})^{10}-9(\dfrac{7}{8})^9-8(\dfrac{7}{8})+7=-0.075$

$f(\dfrac{6}{8})=10(\dfrac{6}{8})^{10}-9(\dfrac{6}{8})^9-8(\dfrac{6}{8})+7=0.8873$

Hence, we can say that the other positive real root of $f$, i.e. $a$, lies between $\dfrac{6}{8}$ and $\dfrac{6}{8}$, i.e. $\dfrac{6}{8}<a<\dfrac{7}{8}$, or a is less than $\dfrac{7}{8}$ and this tells us $g(a)>0$.

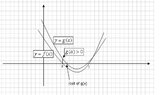
The graph below shows that the real root of $g(x)$ is larger than the root of $f(x)$.

View attachment 1545