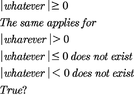SUMMARY
The equation \( |x^2 + 4x| = -12 \) has no real solutions due to the properties of absolute values, which are always non-negative. Algebraically, the analysis involves two cases: when \( x^2 + 4x \ge 0 \) leading to \( x^2 + 4x + 12 = 0 \) and when \( x^2 + 4x < 0 \) resulting in \( -x^2 - 4x + 12 = 0 \). In both cases, the discriminant must be evaluated, confirming that no real solutions exist as absolute values cannot be negative.
PREREQUISITES
- Understanding of absolute value properties
- Familiarity with quadratic equations
- Knowledge of the discriminant in algebra
- Basic algebraic manipulation skills
NEXT STEPS
- Study the properties of absolute values in depth
- Learn how to solve quadratic equations using the discriminant
- Explore the implications of inequalities in algebra
- Review cases in piecewise functions and their applications
USEFUL FOR
Students studying algebra, mathematics educators, and anyone interested in understanding the limitations of equations involving absolute values.