Why don't we find the angular magnification of objective lens in microscopes?

[Shreya]

Homework Statement

I was learning about microscopes & noticed that the lateral (linear) magnification of objective lens is multiplied with the angular magnification of eyepiece. My question is why is the angular magnification of objective not taken?

Relevant Equations

Angular magnification is the ratio of angle subtended by object at eye when viewed through lens to the angle subtended by object when it is placed at near point
$m_\theta = \frac {h}{u} * \frac {D} {h}$

I tried deriving the angular magnification of eyepiece & this is what I got.
$m_\theta = \frac {h}{u} * \frac {D} {h}$
Taking v as $f_0 + L$ from the diagram, I calculated u.
$m_\theta = - \frac{DL} {f_0 (f_0 +L)}$

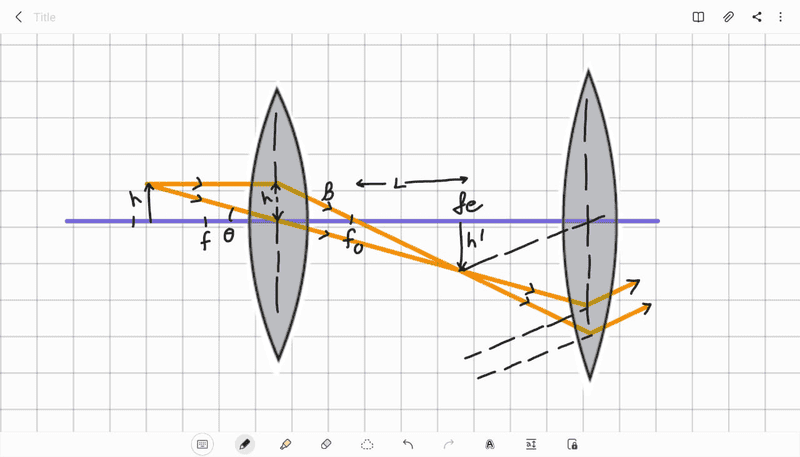
Please verify my calculations and kindly point out my mistakes.

 

[hutchphd]

Sorry, what is D??

 

[Darshit Sharma]

Sorry, what is D??

I guess it is "Least distance for distinct vision" = 25 cm

 

[Darshit Sharma]

View attachment 339745

I know this is off topic but which software is this?

 

[hutchphd]

Where exactly would it appear in your ray traces?

 

[haruspex]

the lateral (linear) magnification of objective lens is multiplied with the angular magnification of eyepiece.

I'm unconvinced by this description of the functions of the two lenses. Seems backwards to me.

There is a good diagram at https://phys.libretexts.org/Bookshe...ge_Formation/2.09:_Microscopes_and_Telescopes
but I don't like the accompanying text, which uses the same division of labour as you quote.

What matters to the eye is

• a large angle subtended at the eye …
• … by an image it can focus on, typically at 25cm or more

According to the diagram, both lenses produce both types of magnification.
The objective lens achieves much angular magnification, largely by making the primary image much closer to the eye, without necessarily having much linear magnification. The eyepiece puts the secondary image at the required distance without changing the subtended angle much, and therefore supplies much linear magnification.

 

[Shreya]

I know this is off topic but which software is this?

I just used Samsung Notes to draw it

 

[Shreya]

The objective lens achieves much angular magnification, largely by making the primary image much closer to the eye, without necessarily having much linear magnification. The eyepiece puts the secondary image at the required distance without changing the subtended angle much, and therefore supplies much linear magnification.

Oh Okay. But, is it okay to multiply linear magnification with angular? What magnification does it give us then?

 

[Shreya]

Where exactly would it appear in your ray traces?

Angular magnification is defined as ratio of the angle subtended at the eye when viewed through the device (microscope) to the angle subtended by the object when kept at least distance of distinct vision - D {without the device}

 

[haruspex]

Oh Okay. But, is it okay to multiply linear magnification with angular?

I don’t think it is. First, what is meant by angular magnification of the objective? As I note, the angle we care about is the angle subtended at the eye. Using that in all cases, the overall angular magnification must be the product of the two angular magnifications. And the two types of magnification are only equal if the image and object are at the same distance.

In the image I linked to, if we assume the eye is very close to the eyepiece, the objective lens gives angular magnification $\frac{h_i(d_o+d_i+d_o')}{hd_o'}$ while the eyepiece gives no angular magnification (the centre of the eyepiece and the tips of the two images lie in a straight line).
Note that that angular magnification is not purely a property of the objective lens. It depends heavily on $d_o'$.

But we should not trust that diagram excessively. The text notes that the objective could have linear magnification up to 100x. In that case, the primary image should be that many times further from the objective than the object is, so the diagram is very much not to scale. So both the linear magnification of the objective and the proximity of the primary image to the eyepiece make significant contributions to the effective angular magnification.

 

[Shreya]

Thanks @haruspex !