SUMMARY
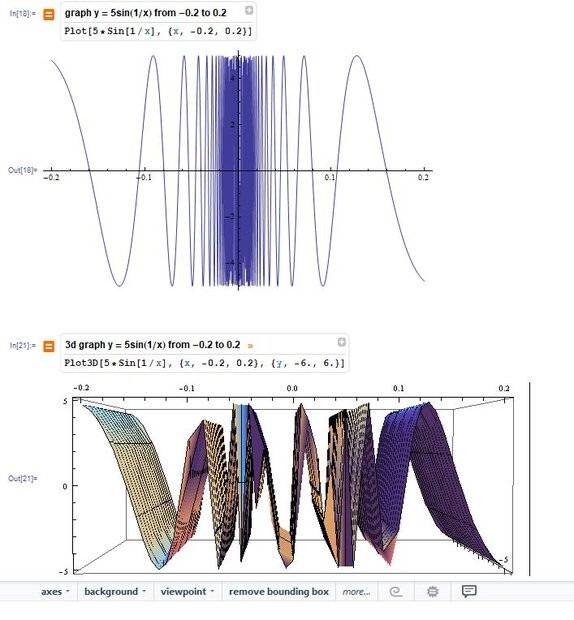
The discussion focuses on the issues encountered when graphing the function y = 5sin(1/x) in 3D using Mathematica. Users noted that the 3D graph does not accurately represent the function due to low sampling rates, leading to aliasing effects. To resolve this, increasing the number of plot points is essential, with suggestions to use Plot3D with PlotPoints set to {10000, 3} and to consider MaxRecursion for functions with rapid changes. The documentation for these features was criticized for being inadequate.
PREREQUISITES
- Familiarity with Mathematica syntax and functions
- Understanding of 3D graphing concepts
- Knowledge of aliasing in signal processing
- Basic experience with mathematical functions and their graphical representations
NEXT STEPS
- Learn how to use Plot3D in Mathematica effectively
- Research the concept of aliasing in mathematical graphing
- Explore the documentation for PlotPoints and MaxRecursion options in Mathematica
- Study advanced graphing techniques in Mathematica for complex functions
USEFUL FOR
Mathematica users, mathematicians, educators, and anyone interested in advanced graphing techniques for complex mathematical functions.