It's fairly simple. First, you need to understand that you can give it almost any shape at an expense of extra tension. I'm sure you've seen all these crazy-looking novelty hot air balloons designed to look like castles, parade floats, or whatever. So the goal should be to have only necessary tension. That means, all of the tension is there to support weight. The most important conclusion you can get from this is that you can consider just a 2D slice across the center of the balloon. So we are looking for that tear-drop shape in a 2D model.
Second, for simplicity, let's assume that the material itself weighs nothing. It isn't true, but you get same qualitative result either way. If you just want to understand why the shape is tear-drop, it's not important. So all of the weight is due to the gondola, and the tension throughout material is constant. Since we are looking at the 2D case, the tension throughout is just half of the gondola's weight. Half, because in 2D the gondola is supported from two sides.
Finally, we look at what's happening to air pressure in the balloon. The hot air balloon is open at the bottom. So at the bottom, the pressure is the same inside and out. However, because density inside is lower, the pressure gradient is lower. That means pressure at the top of balloon is higher. We are going to ignore the fact that as pressure changes, so does density. That's a small correction. So we have now a pressure difference inside and out that's highest at the top and drops to zero at the bottom. That pressure difference will push outward on the balloon at every point.
Now, suppose you have a string under tension. How much force can it apply sideways? That will depend on the curvature. A straight stretch of string will not apply any sideways force. So to support a load, the string must bend. The load perpendicular to the string that stands for the skin of the balloon in the 2D case is due to the pressure. So the surface of the balloon will be most curved where pressure differential is highest. As a result, the top of the balloon will look like the top of a sphere. As you go lower, the curvature will decrease. At the bottom, where pressure differential is almost zero, this wil make a straight line to the gondola.
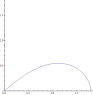
Running all of this through a numerical diff eq solver, I get the following shape. Positive x is "up". Sorry, I didn't rotate it or scale it better.