garcijon
- 1
- 0
Hi All,
This is my first post on these forums. I am not looking for a solution to this problem but more interested in seeing if someone can point me to a resource that can explain the following. Thanks in advance for any help.
I'm trying to solve a pde which gives a temperature profile.
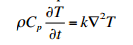
We end up changing over to spherical coordinates where our boundary conditions are not completely clear although our initial condition is.
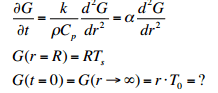
The professor writes something like this. basically it normalizes the boundary conditions to (0,1). I can't wrap my head around this and googling for a while hasn't given me any results that clarify this.
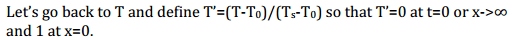
This is my first post on these forums. I am not looking for a solution to this problem but more interested in seeing if someone can point me to a resource that can explain the following. Thanks in advance for any help.
I'm trying to solve a pde which gives a temperature profile.
We end up changing over to spherical coordinates where our boundary conditions are not completely clear although our initial condition is.
The professor writes something like this. basically it normalizes the boundary conditions to (0,1). I can't wrap my head around this and googling for a while hasn't given me any results that clarify this.