Wikipedia shows a proof of product rule using differentials by

[PhDorBust]

Wikipedia shows a proof of product rule using differentials by Leibniz. I am trying to correlate it to the definition of a differential and am having no success.

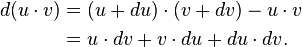
Differential Definition: http://eom.springer.de/D/d031810.htm

 

[Mark44]

Look at how the derivative of a product of functions is derived using the limit of the difference function. The numerator would be u(x + \Delta x) \cdot v(x + \Delta x) - uv.

 

[ross_tang]

You are right up to this step:

d u\cdot v = u \cdot dv + v \cdot du + du \cdot dv

However, if differential is small, differential multiplying to another differential is much smaller, which can be neglected (In limit sense). Therefore:

d u\cdot v = u \cdot dv + v \cdot du

 

[HallsofIvy]

You are right up to this step:

d u\cdot v = u \cdot dv + v \cdot du + du \cdot dv

However, if differential is small, differential multiplying to another differential is much smaller, which can be neglected (In limit sense). Therefore:

d u\cdot v = u \cdot dv + v \cdot du

I would think that the whole purpose of using differentials (which is basically using "non-standard analysis") and developing all the machinary necessary to even define differentials is to avoid saying "in limit sense"! In terms of differentials, the product of two differentials is 0: du\cdot v= u\cdot dv+ v\cdot du directly.

 

[ross_tang]

I agree that differential has the meaning of limit already. But without saying so, it is rather difficult to explain why du dv = 0 in PhDorDust's example. Furthermore, I wonder if product of differentials must be zero, since we sometimes have dx dy in double integral. I think the reason is that, we only need to take the dominating term, which is u dv and v du, but not dv du.