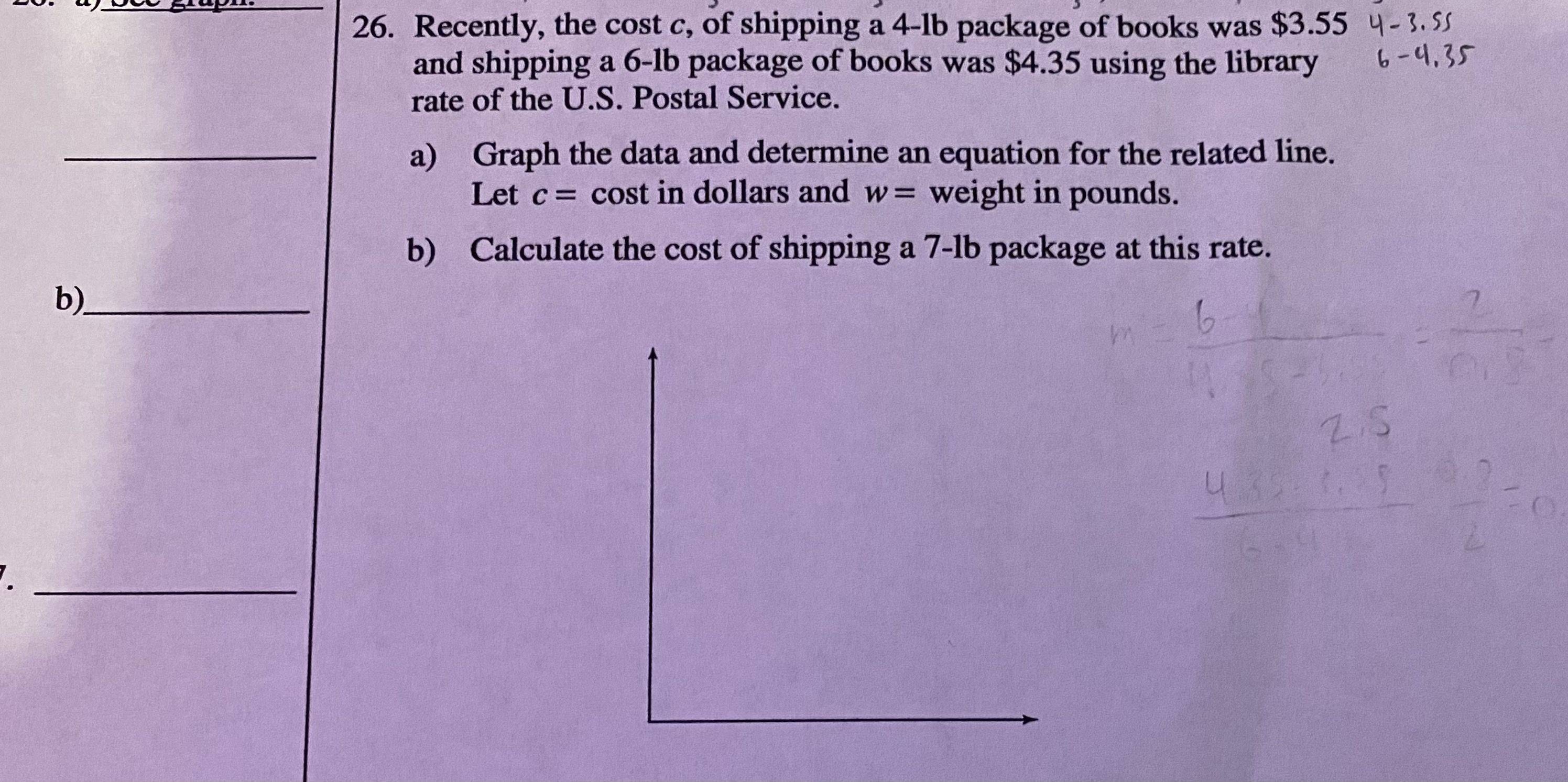
SUMMARY
The discussion focuses on solving a word problem involving the slope-intercept form of a linear equation to determine a shipping cost function based on weight. The two ordered pairs provided are (4, 3.55) and (6, 4.35), from which the slope is calculated as 0.4. The point-slope form of the equation is utilized, specifically the formula $c - c_1 = m(w - w_1)$, to derive the cost function. The final equations to solve for the coefficients a and b are 4a + b = 3.55 and 6a + b = 4.35.
PREREQUISITES
- Understanding of linear equations and their forms, specifically point-slope and slope-intercept forms.
- Basic algebra skills for solving simultaneous equations.
- Familiarity with ordered pairs and their representation in a Cartesian coordinate system.
- Knowledge of dependent and independent variables in mathematical functions.
NEXT STEPS
- Learn how to derive the slope from two points on a graph.
- Study the point-slope form of linear equations in detail.
- Practice solving systems of linear equations using substitution and elimination methods.
- Explore real-world applications of linear equations in cost analysis and pricing models.
USEFUL FOR
Students, educators, and professionals in fields requiring mathematical modeling, particularly those involved in logistics, pricing strategies, and data analysis.