Work in tightening a nut, given max torque and friction torque?

[Kermit_the_Phrog]

Homework Statement

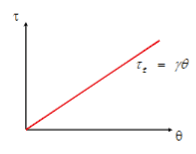
As a nut is tightened through an angle θ , the friction between the nut and the threads on the bolt increases. This causes an increasing frictional torque, Tf = γθ as illustrated. The maximum forces, F, you can apply to the wrench gives a maximum torque Tw. What is the total work you do in tightening the nut?


A. Twθ
B. Tw (Tf/y)
C. (Tw^2)/(2y)
D. (Tw^2)/y

Relevant Equations

W = T θ

NOTE: THIS IS THE GRAPH PROVIDED

At first I approached this problem attempting to solve for the total work done, using the formula

Wtotal = Wmaxforce - Wfriction

I then subbed into the formula, representing the values of work as their torque value times theta, which gave me a longer algebraic solution that was not one of the multiple choice options listed.

ie,

Wtotal = Twθ - Tfθ
= Twθ - (Yθ)θ
= θ (Tw- yθ)

(this is very clearly wrong)

However, now that I've thought about it, the question is phrased in a specific way. It never really asks for the total work, only for the work that YOU do while tightening the nut :

So would it just be

Wmaxforce = T θ
= Tw θ

and thus option A?

Or is the real solution closer to my first approach?

NOTE: i am not really given the final answer so unfortunately I have no idea which final multiple choice answer is correct ¯\_(ツ)_/¯

Thanks in advance!

 

[kuruman]

You need to do an integral because the torque is not constant but depends on the angle. The upper limit of the integral is the final angle which you have to find.

 

[Kermit_the_Phrog]

You need to do an integral because the torque is not constant.

Oh okay, so I'd find the area under the graph of the frictional torque and use that?

 

[kuruman]

Oh okay, so I'd find the area under the graph of the frictional torque and use that?

Yes, that's another way to integrate.

 

[Kermit_the_Phrog]

Yes, that's another way to integrate.

Okay so I took my formula from before and use the integral of the friction torque this time, it gave me this:

Wtotal = Wmaxforce - Wfriction
= Tw θ - (1/2)yθ ^2
= θ (Tw - (1/2)yθ)

which unfortunately doesn't seem to match any of the answers either - did I do something wrong, or am i just missing something?

 

[kuruman]

Wtotal = Wmaxforce - Wfriction

This is incorrect. The maximum torque is a limit and it can be reached only when the nut can no longer be turned. Until that point the torque is less than its maximum value. Forget your formula and go back to finding the area under the curve.

Also, since the nut has zero initial and final angular speeds, the change in kinetic energy is zero. Therefore, by the work-energy theorem, the net work is also zero. Since you and friction are the only agents that do work in this case, the work done by you is the negative of the work done by friction.

 

[Kermit_the_Phrog]

Yes, that's another way to integrate.

okay, thank you for the help.

I think I have an idea though!

If we take the expression I just made, and find its derivative, can we find the value of theta when force is a maximum? (I.E., derive with respect to theta, and solve for the value of theta when W' is zero, then use this value in the original expression to find the value of W?)

I.E.,

W= Tw θ - (1/2)yθ ^2

so

W' = Tw - yθ

Set W' equal to zero

θ = Tw/y

Sub into the first equation

W = Tw (Tw/y) - (1/2)y (Tw/y)^2
= (Tw^2)/y - (Tw^2)/(2y)
= (Tw^2)/(2y)

and thus answer C.

However, upon reading your newest response, I see that the above solution is also likely wrong, so I'll keep working i guess.

 

[Kermit_the_Phrog]

This is incorrect. The maximum torque is a limit and it can be reached only when the nut can no longer be turned. Until that point the torque is less than its maximum value. Forget your formula and go back to finding the area under the curve.

Also, since the nut has zero initial and final angular speeds, the change in kinetic energy is zero. Therefore, by the work-energy theorem, the net work is also zero. Since you and friction are the only agents that do work in this case, the work done by you is the negative of the work done by friction.

Okay, so if the total work is zero, shouldn't the final equation be

Wmaxforce = Wfriction
Twθ = (1/2)y(θ^2)
Tw = (1/2)yθ and at this point, I'm mostly lost, as I'm unaware of what to solve for any more, seeing that the "Wtotal" term no longer exists (its value is zero). (I might be more confused now that I was to begin with)

 

[haruspex]

Wtotal = Wmaxforce - Wfriction

That is for the net work done on the nut. Since it finishes with no angular velocity, this is zero. And you don’t mean Wmaxforce, just Wforce.

Twθ =

It has already been pointed out to you that the work done by the applied torque is not equal to the maximum torque multiplied by the final angle.

 

[Kermit_the_Phrog]

That is for the net work done on the nut. Since it finishes with no angular velocity, this is zero. And you don’t mean Wmaxforce, just Wforce.

It has already been pointed out to you that the work done by the applied torque is not equal to the maximum torque multiplied by the final angle.

Ah, I apologise, I am still learning, and this problem has really got me stumped for some reason. Thanks for bearing with me.

Anyway, in that case, would the work done by the applied torque be it's anti derivative?

 

[haruspex]

would the work done by the applied torque be it's anti derivative?

Yes.

 

[Kermit_the_Phrog]

Yes.

Alright, then I need to find an expression for the maximum torque's anti derivative. However, the question doesn't give me an expression for Tw in the way it does for Tf - Can you point me in the right direction please?

 

[Kermit_the_Phrog]

Yes.

Okay, so I gave it a try any way and set Tw = Fθ, Meaning that its antiderivative would be

1/2F(θ)^2

however, using this in my other calculations didnt get me anywhere, as it did this:

Wforce = Wfriction
1/2F(θ)^2 = (1/2)y(θ^2)
so F =y

Which hit a dead end pretty quickly, since this expression didn't lead me anywhere in my calculations.

Man, i don't think this problem is supposed to be this hard, I feel like I am missing something obvious

 

[kuruman]

The work done by torque $\tau=y\theta$ is $$W=\int_0^{\theta_{max}}\tau~d\theta.$$Find $\theta_{max}$ in terms of $T_w$, then integrate. It's that simple.

 

[Kermit_the_Phrog]

The work done by torque $\tau=y\\theta$ is $$W=\int_0^{\theta_{max}}\tau~d\theta.$$Find $\theta_{max}$ in terms of $T_w$, then integrate. It's that simple.

Okay, I am with you on the integration part, but how do I relate Tw and θmax?

 

[kuruman]

If the general expression for the torque is $T_f=y\theta$, what is the specific expression for the torque when $\theta=\theta_{max}$?

 

[Kermit_the_Phrog]

If the general expression for the torque is $T_f=y\theta$, what is the specific expression for the torque when $\theta=\theta_{max}$?

In that case,

Tf = y θ

so

Tfmax = yθmax ?

which rearranges to give

θmax = Tfmax/y

If I am correct, then I should integrate the first expression now:

W = (1/2)y(θmax)^2

I then sub in the equation for θmax:

W = 1/2y(Tfmax/y)^2
=(Tfmax)^2/2y

Which is very close to answer C EXCEPT for the fact that it's in terms of Tfmax and NOT Tw. I'm guessing that these terms are equal in this case? If they are, that would make the proof work perfectly, but is this assumption unwarranted? How do I prove that Tfmax = Tw?

oh and many thanks for helping me all this way, I really appreciate it !

[Though I'm feeling pretty foolish now, seeing that the answer was that simple... :( ]

 

[kuruman]

From the problem statement

The maximum forces, F, you can apply to the wrench gives a maximum torque Tw.

Tfmax is your invention; it is not given by the problem.

 

[Kermit_the_Phrog]

From the problem statement

Tfmax is your invention; it is not given by the problem.

Hang on, if net work is zero, does net torque have to be zero too?

If that's true, then

0 = Tw - Tfmax

and therefore,

Tw = Tfmax , which works with my solution

Is this correct?

 

[Kermit_the_Phrog]

From the problem statement

Tfmax is your invention; it is not given by the problem.

And I know that, but I can't simply take the expression

Tf = yθ

and replace Tf with Tw when I sub in θmax: the two terms are not necessarily the same, right?

Thus, I made a term for the torque of friction when theta is at its maximum, titled "Tfmax" as a place holder

 

[Kermit_the_Phrog]

From the problem statement

Tfmax is your invention; it is not given by the problem.

Or is it simpler than this? we just assume that the made up term "Tfmax" is equal to the term "Tw" because the question states:

"The maximum forces, F, you can apply to the wrench gives a maximum torque Tw"

Thus, since Tfmax occurs when the force of friction is a maximum, it would give a "maximum torque Tw"?

Is it really that simple?

 

[kuruman]

And I know that, but I can't simply take the expression

Tf = yθ

and replace Tf with Tw when I sub in θmax: the two terms are not necessarily the same, right?

Thus, I made a term for the torque of friction when theta is at its maximum, titled "Tfmax" as a place holder

$T_f$ is a placeholder for any torque less than the maximum and $T_w$ is a placeholder for the maximum torque that you can apply to the nut. There is only one maximum value but many torque values less than that maximum. The problem called the placeholder for the maximum $T_w$ but you chose to rename it Tfmax. That's all.
$$Torque =
\begin{cases}
0, & \theta =0 \\
y\theta, & 0 \lt \theta \lt \theta_{max} \\
T_w, & \theta = \theta_{max} \\
\end{cases} $$

 

[Kermit_the_Phrog]

That's all.

Man, I really over thought this, huh.

 

[kuruman]

Or is it simpler than this? we just assume that the made up term "Tfmax" is equal to the term "Tw" because the question states:

"The maximum forces, F, you can apply to the wrench gives a maximum torque Tw"

Thus, since Tfmax occurs when the force of friction is a maximum, it would give a "maximum torque Tw"?

Is it really that simple?

Yesssss! It's that simple.

 

[Kermit_the_Phrog]

Yesssss! It's that simple.

Thanks again by the way - I really do appreciate the help. Enjoy the rest of your day, and you're the best.