Sammywu said:
If
[1] \sum_n a_n P_{e_n} = P_{\sum_n a_n e_n} ...
The object on the left-hand-side is not (in general) a projector. That object has eigenvalues a
n , whereas a projector has eigenvalues
0 and / or 1.
--------------------------
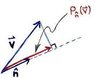
At this juncture, it is instructive to consider ordinary 3-D Euclidean space. Pick any unit vector
n. Then, the projector corresponding to this unit vector is given by
[2] P
n(
v) = (
v∙
n)
n , for any vector
v .
The description of [2] is "the projection of
v along
n". Do you remember what this means geometrically? (see
figure).
--------
NOTE:
In Dirac notation, [2] becomes
P
n|v> = <n|v> |n> = |n> <n|v> = (|n><n|) |v> , for any |v> .
We therefore write:
P
n = |n><n| .
If you think of each ket as a column matrix and the corresponding bra as its Hermitian transpose (a row matrix) then this notation can be taken "literally".
--------------------------
I suggest you reserve the symbol "P", in the above type of context, only for a "projector"
proper. Also, I suggest you invoke the rule that the "subscript" of P is always a
"unit" vector. These two prescriptions would then disqualify the "legitimacy" of the right-hand-side of [1] on
both counts.
At the same time, if you want to consider generalizations for which a relation like [1] holds, then use a symbol "R" (or whatever else)
instead of "P". The generalization of [2] which gives a relation like [1] is then simply:
[2'] R
u(
v) = [
v ∙ (
u/|
u|) ]
u , for any vector
v .
But what is the motivation for reserving a special "symbol" for this operation? Its description is
"project the vector v into the direction of u and then multiply by the magnitude of u". The meaningful aspects of this operation are much better expressed by writing the corresponding operator as |
u|P
(u/|u|).
--------------------------
Now, let's go back the definition I gave in post #2.
Definition: P is a "projector" if (and only if):
(i) Pt = P ,
and
(ii) P has eigenvalues 0 and/or 1 .
It then follows that P is a "projector" if, and only if, Pt = P and P2 = P.
I am now
strongly suggesting that we, instead, use the following as our "official" definition:
*************************
* 1a) Given any unit vector
e, definite the "projector onto
e" by:
*
* P
e(
v) = (
v,
e)
e , for any vector
v .
*
* Such a projector is said to be "1-dimensional".
*
* 1b) An operator P is said to be a "projector" if (and only if)
* it can be written as a sum of 1-dimensional projectors
* which project onto mutually orthogonal unit vectors.
*
*************************
This definition [1a) and 1b) taken together] is equivalent to the original one I gave. But I think it makes the
meaning of "projector" much clearer.
------------------------------------------------------
All that I have said above should clarify matters like:
Sammywu said:
But 2 P_{e_n} does not seem to be the projector for
2 e_n ...
-----------