Forces involved in a 'tug of war'

[bobie]

Can someone give a detailed phusical description description of the forces involved in this game?
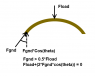
Let consider only the first player on the right:

0) does it make any difference if he is pulling aagainst an opposing varying force or he is pulling a truck?
---
1) does friction play any role here? if his heels are dug in a hole or lean on a reversed starting block, does it make any difference?
2) his legs are fully stretched. Can he exert a force directly on the ground?
3) can he exert a greater force either on the rope or on the ground
4) if yes, how
5) if no, is it due to Newton third law? suppose his legs are stretched and the ground is just a point of support: when he pulls the rope is half force discharged on the ground?
6) if he wants the rope to accelerate in his direction is it necessary that the two forces be unequa? Is it true that if they are equal the total force on the player will vanish?

6) in conclusion, after all your evaluations which force is more important for victory, the one on the rope or the one ond the ground

Thanks in advance, it would be great to have a sketch of the forces in play showing how forces are discharged to the ground.

 

[A.T.]

What are your own thoughts on the questions?

 

[bobie]

What are your own thoughts on the questions?

I think
- the friction plays no role if foot is dug in. I am posting because I read that even if it is in a hole or on a staring block it is relevant.
- with stretched legs you cannot push directly on the ground. If you push the force can never be greater then the pull on the rope.
- wherevere you exert a force, as you must prop up on the opposite side, you discharge half of the force on the other side by 3rd law. But also in this regard I read that if the force on the ground and the rope are equal there can be no acceleration, motion of the rope toward you

Thanks for your attention

 

[A.T.]

I think
- the friction plays no role if foot is dug in. I am posting because I read that even if it is in a hole or on a staring block it is relevant.

What if the hole is shallow, so the effective surface you push against is not perpendicular to gravity + rope force?

with stretched legs you cannot push directly on the ground.

But the question was if he "exerts a force on the ground". If he didn't what would be the horizontal net force on him and thus his acceleration?

If you push the force can never be greater then the pull on the rope.

Are you talking about total magnitudes, or just the horizontal components? Can you win the game if the horizontal components are always equal.

- wherevere you exert a force, as you must prop up on the opposite side, you discharge half of the force on the other side by 3rd law.

Where does 3rd law talk about "half of the force"?

But also in this regard I read that if the force on the ground and the rope are equal there can be no acceleration, motion of the rope toward you

What does 2nd law say about this?

 

[bobie]

What if the hole is shallow, so the effective surface you push against is not perpendicular to gravity + rope force?
But the question was if he "exerts a force on the ground". If he didn't what would be the horizontal net force on him and thus his acceleration?
Are you talking about total magnitudes, or just the horizontal components? Can you win the game if the horizontal components are always equal.
Where does 3rd law talk about "half of the force"?
What does 2nd law say about this?

Thanks for asking me so many questions, but what are your answers?

What has gravity got to do here? why has the hole to be deep or perpendicular , ( what matter is if it blocks your foot)? how do you exert directly a force on the ground if you do not stretch your legs (the force on the ground is exerted mainly by the opponent)? and what about 2nd law here? how do you get an acceleration if not pulling on the rope? if you do not answer the 0 question I do not have a clear picture.

 

[A.T.]

What has gravity got to do here?

Why don’t you sketch all the forces acting on the man?

why has the hole or the starting block to be perpendicular?

Who said it has to be perpendicular? The question was when friction becomes necessary. To see this draw a diagram with all the forces and the ground contact surface.

how do you exert directly a force on the ground if you do not stretch your legs?

When you just stand around with already stretched out legs, do you exert a force on the ground?

and what about 2nd law?

Can the rope accelerate if it has equal but opposite force on both ends?

 

[bobie]

Why don’t you sketch all the forces acting on the man?
Who said it has to be perpendicular? The question was when friction becomes necessary. To see this draw a diagram with all the forces and the ground contact surface.
When you just stand around with already stretched out legs, do you exert a force on the ground?
Can the rope accelerate if it has equal but opposite force on both ends?

I am not able to draw and post a sketch, that is why I asked for it in OP.

You are confusing me even more. Force on the ground must be exerted horizontally to win the game, what is the use of g?
I begged you twice, start with the truck, which is simple: to pull a truck you pull horizontally on the rope and prop up your feet to an obstacle in/on the ground. Do you exert a force directly on the obstacle or just as a consequence of the pull on the rope? suppose you use 100 N, how much of this is discharged on the obstacle, if not 50%? what determines this percentage?
If you discharge 50% of the force , 50 N, on the ground you have two equal forces, but no work is done on the ground so you can have an acceleration on the rope, what is the problem?

 

[A.T.]

Force on the ground must be exerted horizontally to win the game,

Can the force on the ground be purely horizontal under gravity?

start with the truck, which is simple:

It's not that simple to beat a truck that uses it's engine. With engine off the truck can at best get a tie.

 

[bobie]

It's not that simple to beat a truck that uses it's engine. With engine off the truck can at best get a tie.

I mentioned no engine. But I suppose you can't tell more on the subject.

 

[A.T.]

I mentioned no engine.

Then it depends on how deep the truck will sink into the mud. On asphalt even a single human can pull a truck, with decoupled wheels and brakes off.

 

[sophiecentaur]

@bobie
I agree with AT. You need to draw a very simplified model - two guys and a rope - and draw in the forces. In the equilibrium situation, clearly, both guys must be pulling with the same force (= tension in rope). If one guy is stronger or the other guy has less traction, there will be no longer be equilibrium.
As OP, it is really up to you to draw the diagram and present it, otherwise we do not know what we are supposed to be discussing. There are dozens os drawing utilities available and, if you 'Go Advanced', you can find how to upload a file - there is a big choice of formats that are accepted.

 

[bobie]

Thanks sophiecentaur, my main concern is not the equilibrium of forces, that is why I insisted on the truch, which does not pull.
My question cannot be answered by a drawing, but only by one expert physicist like you. I want to know how much of the force I exert goes really to the truck and how much is lost, doing no work on the ground, and if this percentage can be altered and why.
Is it clear now?

I'll appreciate even a brief reply with just the percentages. My assumption 50-50% has been rejected.

 

[sophiecentaur]

Thanks sophiecentaur, my main concern is not the equilibrium of forces, that is why I insisted on the truch, which does not pull.
My question cannot be answered by a drawing, but only by one expert physicist like you. I want to know how much of the force I exert goes really to the truck and how much is lost, doing no work on the ground, and if this percentage can be altered and why.
Is it clear now?

I'll appreciate even a brief reply with just the percentages. My assumption 50-50% has been rejected.

There a some basics that you must accept first. You can only find an answer if you examine what forces are operating. I could not hope to start on such a problem without drawing a diagram. Unless you do, you risk missing out something relevant.
A force is not "lost". No work is done on anything unless there is movement involved. Man pulls truck truck provides exactly the same amount of force on rope. There's no "50%/50% involved (as a diagram would show, aamof). The forces around the man are a bit more complex because he is leaning backwards. There is his weight, friction and the rope tension. (Diagram again) all acting at different places and establishing equilibrium (unless he moves the truck).
You just can't do this one by waving arms around (any more than the guy with the rope. )

 

[bobie]

Thanks for your help, probably this is to complicated for me.

 

[PhanthomJay]

Thanks for your help, probably this is to complicated for me.

Assuming no hand slippage, the tension in the rope is the same pulling on each team. Although there are complexities involved, friction/traction of feet on ground is key. If one team is on ice and the other on soil, I bet you know who wins.

 

[sophiecentaur]

The diagram I had in mind is below (jeez, I'm good to you, aren't I?)This is the essence of the one man pulling a rope attached to 'something' and I am assuming that things are in equilibrium, for a start. It assumes the man is strong enough to provide the tension and the leg thrust and that the friction with the ground is enough to hold him. To work out the tension, you need to consider the Moments about a point (choose his contact point with the ground). The moment of the tension will be equal and opposite to the moment of his weight. He will need to be at the correct angle to the ground for this. The calculation involves some Trig - but I have left it out, initially.
There are just two horizontal forces here, so T will equal R.

If he is 'winning' then T will be enough to drag the truck and he will need to be walking backwards, so he does T times x work, where x is the distance moved. I assume the truck is moving very slowly and not accelerating appreciably. All the work done is against friction. If he is actually managing to produce significant acceleration then you would need to include the kinetic energy situation too.

If T increases then he needs to lean back more and the friction needs to be high enough or he will fall on his backside or start 'surfing' through the mud (if he can control it).

PS Powerpoint is easy to use to produce this simple diagram -once you get used to it.

 

[A.T.]

PS Powerpoint is easy to use to produce this simple diagram -once you get used to it.

There are also many free online sketching tools, where you draw in the browser and get a link to your drawing for posting here on the forum.

 

[A.T.]

I am assuming that things are in equilibrium, for a start.

How can those forces be in equilibrium, if the ground reaction acts only horizontally?

 

[Dale]

Thanks sophiecentaur, my main concern is not the equilibrium of forces, that is why I insisted on the truch, which does not pull.
My question cannot be answered by a drawing, but only by one expert physicist like you. I want to know how much of the force I exert goes really to the truck and how much is lost, doing no work on the ground, and if this percentage can be altered and why.
Is it clear now?

I'll appreciate even a brief reply with just the percentages. My assumption 50-50% has been rejected.

Forces do not work this way. You are thinking of something which is conserved and so you can say that 50% goes here and 50% goes there. Forces are not conserved. For example, on a simple lever you may exert a force of 10 N and get out a force of 100 N. Talking about "lost" or "percentage" of force just doesn't have any physical meaning. That is probably why you are not getting good answers to that part of your question.

 

[sophiecentaur]

How can those forces be in equilibrium, if the ground reaction acts only horizontally?

The reaction R against the Tension is horizontal. Of course there is another vertical force to balance weight etc.
I could put more arrows in - plus angles and distances etc. But this is a very stock 'Forces' situation. Other well known ones are ladders leaning against walls and men pushing wheelbarrows. Once you've seen and done one, you've seen 'em all.

 

[sophiecentaur]

There are also many free online sketching tools, where you draw in the browser and get a link to your drawing for posting here on the forum.

Drawing (object based), rather than sketching is better for a good diagram. You can edit: move and rotate objects and avoid wiggly lines and mouse / hand writing. A very little investment in getting to use a drawing package will make you happy - and everyone else on PF.

 

[A.T.]

The reaction R against the Tension is horizontal.

R is not the reaction to tension. R is the reaction to the force that the foot applies to the ground.

Of course there is another vertical force to balance weight etc.

If you put the weight into the diagram, then you should also put in the vertical ground reaction force. Otherwise there can be no balance.

I could put more arrows

You can also draw the total ground reaction at an angle. The direction of that vector it relevant for the question regarding the need for friction:

1) does friction play any role here? if his heels are dug in a hole or lean on a reversed starting block, does it make any difference?

 

[bobie]

Forces do not work this way. You are thinking of something which is conserved and so you can say that 50% goes here and 50% goes there. .

No, I was not thinking that. I have little experience but I was thinking of an arc, a vault. When you exert a vertical force on a bridge, an arc most of it is discharged horizontally, that is why a fortress has flying buttresses. Now, when you pull on the rope and on the truck you have to prop up to the ground, and , I thought, you must discharge some force on the ground.

Is that a wrong deduction?

 

[A.T.]

Now, when you pull on the rope and on the truck you have to prop up to the ground, and , I thought, you must discharge some force on the ground.

Forces are "exerted" or "applied" not "discharged". When a book rests on the table, it can exert a force on the table indefinitely, without the need to ever "recharge", so it is misleading to talk about "discharging" forces.

If you are in balance (not accelerating) then all the forces you exert must sum to zero. So if you pull the rope with some horizontal force, you must exert an equal but opposite horizontal force on something else, like the ground.

 

[bobie]

Forces are "exerted" or "applied" not "discharged".

2) if you pull the rope with some horizontal force, you must exert an equal but opposite horizontal force on something else, like the ground.

1) not discharged, what then, deviated? how do you account for the force pushing a wall laterally when a force is applied vertically to arc? where does it come from?

2) if you apply a force of 300N to the rope/train how can you apply an equal extra 300N force on the ground? wouldn't that add up to 600N?

That is exactly what I said and was rejected:

wherevere you exert a force, as you must prop up on the opposite side, you discharge half of the force on the other side

That is what I meant : 150 + 150 N, now you say 300+300N, but the principle is the same, maybe it is not due to 3rd law, but the concept is evident, undeniable anyway.

 

[A.T.]

Forces are "exerted" or "applied" not "discharged".

1) not discharged, what then, deviated?

Read again. I told you two common terms.

if you pull the rope with some horizontal force, you must exert an equal but opposite horizontal force on something else, like the ground.

2) if you apply a force of 300N to the rope/train how can you apply an equal extra 300N force on the ground? wouldn't that add up to 600N?

Read again. it says "equal but opposite", not "equal". Two equal but opposite forces add up to zero.

 

[bobie]

Read again. I told you two common terms.
Read again. it says "equal but opposite", not "equal". Two equal but opposite forces add up to zero.

You said 'exerted' 'applied', but on an arc the applied/exerted force is vertical, how much of it goes horizontal ? and are you saying this is the applied force? that you applied force laterally?

2) the point is that here the sum is not 0: you have a net force of 300 N applied to the truck whose reaction is -300N, then it the truck does not budge you have the equilibrium.
But you said literally

"So if you pull the rope with some horizontal force, you must exert an equal but opposite horizontal force on something else, like the ground."

if those forces add up to zero you are not exerting any force on the truck.
Moreover if you are standing at 45% you are not exerting the force horizontally on the ground but at 45° and the horizontal component is 300* cos λ =210 N, right?

 

[CWatters]

No, I was not thinking that. I have little experience but I was thinking of an arc, a vault. When you exert a vertical force on a bridge, an arc most of it is discharged horizontally, that is why a fortress has flying buttresses...

The arc or buttress changes the angle the force makes with the ground BUT it also increases the total forces on the ground.

The vertical component of the force on the ground ends up unchanged. It has to be because if the bridge isn't [STRIKE]moving [/STRIKE] accelerating vertically the vertical forces on it must still sum to zero.

 

[CWatters]

Moreover if you are standing at 45% you are not exerting the force horizontally on the ground but at 45° and the horizontal component is 300* cos λ =210 N, right?

I think you have that the wrong way around.

If you aren't [STRIKE]moving[/STRIKE] accelerating the horizontal component of the force you exert on the ground must be equal to the tension in the rope eg 300N. So the total force your legs must exert at 45 degrees must be higher..

Compression Force in legs * cos(45) = 300

Compression Force in legs = 300/cos(45) = 424N

If you don't apply 424N at 45 degrees the horizontal component can't be 300N and you will be [STRIKE]moving [/STRIKE]accelerating one way or the other.

 

[A.T.]

but on an arc the applied/exerted force is vertical, how much of it goes horizontal ? and are you saying this is the applied force? that you applied force laterally?

What CWatters said.

you have a net force of 300 N applied to the truck whose reaction is -300N, then it the truck does not budge you have the equilibrium.

No, because those two forces act on different objects. It makes no sense to add them up. See:
https://www.lhup.edu/~dsimanek/physics/horsecart.htm

if those forces add up to zero you are not exerting any force on the truck.

No. If the forces on you add up to zero then you are not accelerating. You still exert a force on the rope/truck.

Moreover if you are standing at 45% you are not exerting the force horizontally on the ground but at 45° and the horizontal component is 300* cos λ =210 N, right?

If the force of the rope on you is 300N and you are not accelerating, then the horizontal ground reaction component on you is -300N. They add up to zero.

 

[A.T.]

If you aren't moving the horizontal component of the force you exert on the ground must be equal to the tension in the rope eg 300N.

This should be "accelerating" not "moving". You can be moving at constant speed with balanced forces. But otherwise CWatters explained it well.

 

[CWatters]

This should be "accelerating" not "moving". You can be moving at constant speed with balanced forces. But otherwise CWatters explained it well.

Thanks. Was just in the process of changing that.

 

[CWatters]

Perhaps a diagram..

 

[bobie]

Perhaps a diagram..

That diagram is precious, can you add gravity (man's weight 100Kg) and insert it in your post so that I can copy, using the quote button. Or , is g already included in the diagram and that's why we get 424N?

Thanks a lot, CWatters

 

[bobie]

The arc or buttress changes the angle the force makes with the ground BUT it also increases the total forces on the ground.

The vertical component of the force on the ground ends up unchanged. It has to be because if the bridge isn't [STRIKE]moving [/STRIKE] accelerating vertically the vertical forces on it must still sum to zero.

If I got it right you are saying that if I apply a downward force of 300N on the arc, all of 300N end up on the ground, but some force is exerted on the walls horizontally, suppose the arc is a perfect semicircle, what is the intensity of this lateral force, and where does it come from? can the result of a force be grater than 100%?

 

[A.T.]

where does it come from?

The vector sum of the lateral forces is zero. A zero force doesn't have to "come from somewhere".

can the result of a force be grater than 100%?

The lateral forces can be greater than the vertical one. Instead of an arc, consider a simple roof:

/\

What will be the ratio of horizontal to vertical forces when the slopes are less than 45°?

 

[CWatters]

If I got it right you are saying that if I apply a downward force of 300N on the arc, all of 300N end up on the ground, but some force is exerted on the walls horizontally, suppose the arc is a perfect semicircle, what is the intensity of this lateral force, and where does it come from?

If it's a perfect semi circle the ends meet the ground at 90 degrees so there is no horizontal force on the ground. If it's only an arc (as per my diagram) then yes there is a horizontal force. The intensity is Fgnd*sin(theta)

can the result of a force be grater than 100%?

Yes. It can be infinite.

What is the tension in a washing line or telephone wire? How much tension is needed to make the wire perfectly horizontal not hanging in a curve... Try hanging a brick from the middle of some string. Then lift the brick by pulling the ends of the string apart horizontally. How much force is required to make the string perfectly straight and horizontal? Are you strong enough :-)

 

[bobie]

If it's a perfect semi circle the ends meet the ground at 90 degrees so there is no horizontal force on the ground.

Suppose the semicircle (50Kg) is on a weighing platform, if you put on top of it a weight exerting 100N, all force goes laterally, no force on the platform, the recorded weight is still 50Kg?

 

[CWatters]

That diagram is precious, can you add gravity (man's weight 100Kg) and insert it in your post so that I can copy, using the quote button. Or , is g already included in the diagram and that's why we get 424N?

I could but it's better to do that on another diagram showing the torques acting on the man.

Lets assume the man isn't falling over. eg he is not rotating about his feet. (Technically I should say that he's not subject to rotational acceleration). To meet that condition the sum of the torques about his feet must also add to zero. So the anticlockwise torque due to his weight must equal the clockwise torque due to the tension in the rope.

I also have to make some assumptions about how high up the man the rope is attached and where his centre of mass is. Let's say that the rope is attached to the man at height h_r when he is stood up. So it's at h_r*sin(theta) above his feet when he leans at theta. Likewise his centre of mass is at h_m when he is stood up straight and h_m*sin(theta) when he is leaning.

Note that _if_ m,g,h_r and h_m are constants then in order to apply 300N he must lean at the correct angle which might not be 45 degrees. I'll let you substitute values and solve for theta.

If you insist the man must lean at 45 degrees then he would have to change h_r to make the torques sum to zero. Otherwise he will either fall or be pulled upright. (edit: or he cannot apply 300N to the rope, something must change to ensure the torques sum to zero).

In short if he's not accelerating (be it linear or rotational acceleration) then

The vertical forces must sum to zero
The horizontal forces must sum to zero
The torques must sum to zero.

 

[CWatters]

Suppose the semicircle (50Kg) is on a weighing platform, if you put on top of it a weight exerting 100N, all force goes laterally, no force on the platform, the recorded weight is still 50Kg?

If it's a perfect semi circle no force goes laterally it all goes vertically!

You also made some errors in the units. 50kg = 500N approx. So total force is..

500+100=600N

This would be split 300N on each side of the bridge.

If the scale is under both sides at the same time it will be subject to 600N vertically and read 60kg.

 

[CWatters]

If the semi circle was not perfect/full then there would be a lateral force that tried to stretch the scale horizontally. vertical scales do not measure horizontal forces. So the scale would still read 60kg (edit: because the vertical forces must still sum to zero, the scale isn't accelerating).

 

[CWatters]

Do try the experiment with a brick on a string (see post #37 above). Better still try it while standing on some scales. No matter how hard you have to pull on the string to try and get it horizontal the reading on the scales won't change.

 

[bobie]

Note that _if_ m,g,h_r and h_m are constants then in order to apply 300N he must lean at the correct angle which might not be 45 degrees. I'll let you substitute values and solve for theta.

If you insist the man must lean at 45 degrees then he would have to change h_r to make the torques sum to zero. Otherwise he will either fall or be pulled upright. (edit: or he cannot apply 300N to the rope, something must change to ensure the torques sum to zero).
.

The diagram is great but vanishes when I quote. Can you place one somewhere on the web so that I can pick it up?
There is something I still do not understand:
there is no horizontal force on the ground in this sketch
if the man's weight is 100 kg , then the force of g is 1000N right?
so the force of 300N is unrealistic? any ideas what pulling force a strong man of 100Kg can exert?
now there is a downward force of 1000N applied roughly at man's stomach, shouldn' t it be split in 2 parts and one shouldn't be tangential, as it is a torque, and the other along the body??
isn't the force he exerting on the groung along the same line of the body, and shouldn'it be split, again, by a parallelogram?
why can't he stand at 45° as long as the truck doesn't move??

Thanks Cwatters, you are very patient and helpful. I regret the system doesn't allow me to send any more thanks.

 

[Dale]

No, I was not thinking that. I have little experience but I was thinking of an arc, a vault. When you exert a vertical force on a bridge, an arc most of it is discharged horizontally, that is why a fortress has flying buttresses. Now, when you pull on the rope and on the truck you have to prop up to the ground, and , I thought, you must discharge some force on the ground.

Is that a wrong deduction?

If you were not thinking about conservation of force then you should definitely watch your wording. Even here, your wording strongly carries the impression that you think forces are conserved.

You talk about "discharging" forces. Charge is conserved. Once you have discharged a capacitor there is no more charge. Use of the word "discharge" is confusing if you do not intend to convey conservation.

I would recommend using the standard terms "exert" or "apply". To calculate how much force is exerted on the ground, I would start with the free-body diagram provided by sophiecentaur, except that the reaction force on the ground is at an angle θ instead of horizontal, or the free-body diagram provided by CWatters, except with the weight.

 

[Dale]

But you said literally if those forces add up to zero you are not exerting any force on the truck.

Despite your protestations to the contrary, to me it sounds like you really think that forces are a conserved quantity. I cannot see how to make sense of this comment without assuming you are thinking of conservation of force.

 

[Dale]

There are three forces acting on the man. Gravity is exerting a force of mg vertically downwards. The tension is exerting a force T horizontally. The ground is exerting a force R at an angle of θ from the ground.

Assuming that the man is not accelerating then by Newton's 2nd law we can write algebraic expressions relating the vertical and horizontal components of R to T and mg. Using those two equations you can solve for θ and R in terms of T and mg.

Why don't you try that?

 

[Dale]

The torques must sum to zero.

That is interesting. There must be some extra degree of freedom then, because otherwise the system is overdetermined.

 

[bobie]

Despite your protestations to the contrary, to me it sounds like you really think that forces are a conserved quantity. I cannot see how to make sense of this comment without assuming you are thinking of conservation of force.

Yes and no, Dalespam. I have little technical knowledge, write in a foreign language, therefore do not make myself understood.
No, I use discharge as when you discharge a shot, a blow. You apply a force vertically, but all or some is deviated in an other direction: 70% down and 30% sideways.
Yes I think of a force as coming from energy and producing energy. If this means 'conserved' I believe so. I cannot imagine, bar form 'tricks' of some kinds, like a lever etc. that you apply a 300N F and you in the end find yourself with 290 or 310.
If I am in space between to rocks and I stretch my body pushing on both and You say I exert a force of 300 N I take it that my overall 'power' is 300N, so if the rocks move (or not) I expect them to move at different speeds but according to 3rd law and working out in reverse the values I can find that I exerted 60% on one and 40% on the other, but the total force I applied must be 100%

What is wrong with this, it is rational, perhaps it doesn't follow the valid definitions?

That is why I cannot follow you when you say I exert 300N, 300 on the rope and 300 on the ground.
I'd appreciate if at last, you make me understand.

 

[A.T.]

Yes I think of a force as coming from energy and producing energy.

No, it isn't. When a book rests on the table, it can exert a force on the table indefinitely, without any input of energy.

my overall 'power' is 300N

Power is not measured in Newtons.

What is wrong with this,

You have basic misunderstandings about what forces are.

 

[bobie]

No, it isn't. When a book rests on the table, it can exert a force on the table indefinitely, without any input of energy.

Are you sure g is not working fulltime?