Forces involved in a 'tug of war'

[Nugatory]

Are you sure g is not working fulltime?

Quite sure. There's no energy entering or leaving the system.

 

[olivermsun]

g is working full time, but the physical quantity of "work," which is basically transfer of mechanical energy to the table, is zero. The book is not increasing the kinetic or potential energy of the table just by sitting on top of it.

 

[Dale]

Yes and no, Dalespam. I have little technical knowledge, write in a foreign language, therefore do not make myself understood.
No, I use discharge as when you discharge a shot, a blow. You apply a force vertically, but all or some is deviated in an other direction: 70% down and 30% sideways.

Again, there is no conservation of forces so there is no reason that the "down" and "sideways" forces should add up to 100%. I am sorry, but everything you say confirms that deep down you have this idea that forces should be conserved.

There certainly could be a language barrier, but I think you have a concept wrong in addition to the language barrier.

Yes I think of a force as coming from energy and producing energy. If this means 'conserved' I believe so. I cannot imagine, bar form 'tricks' of some kinds, like a lever etc. that you apply a 300N F and you in the end find yourself with 290 or 310.

This is simply wrong. First, if your concept of force has to consider a lever to be a "trick" which operates outside the normal laws of forces then it is clear that your concept of force is wrong. With a lever I can apply 300 N and get 3000 N, quite easily. Even a simple inclined plane can change a 300 N horizontal force into a 3000 N vertical force. Others have mentioned how cables at shallow angles can exert immense horizontal forces in response to small vertical forces.

If I am in space between to rocks and I stretch my body pushing on both and You say I exert a force of 300 N I take it that my overall 'power' is 300N, so if the rocks move (or not) I expect them to move at different speeds but according to 3rd law and working out in reverse the values I can find that I exerted 60% on one and 40% on the other, but the total force I applied must be 100%
What is wrong with this, it is rational, perhaps it doesn't follow the valid definitions?

The same as above. Forces are simply not conserved. It doesn't make any sense to think of them in terms of percentages and so forth. You must simply let go of that idea.

Forces follow Newton's 3 laws. The proper way to analyze and understand forces is to draw free-body diagrams, and apply Newton's laws to them, as well as the usual rules of vector addition and decomposition.

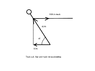
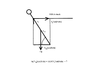
As I said above, the free body diagram for the man has 3 forces acting on it, the force of gravity of magnitude mg pointing down, the tension force of magnitude T pointing horizontally, and the ground reaction force of magnitude R pointing diagonally upwards at an angle of θ from the ground.

The vector sum of those three forces is equal to ma as stated by Newton's 2nd law. From that, if you know those three forces then you can determine the acceleration, or if you know the acceleration you can determine those forces.

That is how you analyze forces, you use Newton's laws. No percentages enter in anywhere.

 

[bobie]

Again, there is no conservation of forces so there is no reason that the "down" and "sideways" forces should add up to 100%.
This is simply wrong. First, if your concept of force has to consider a lever to be a "trick"

Thanks for your explanations, before I understand that I need to clarify what is probably misleading me:
1) isn't impulse a force? (I thought the only difference is that a force acts indefinitely and an impulse a short time) if that it is true can we substitute one with other?

2) I can't quote CWatter's picture, I can't yet post a diagram, so look at this:

- Roughly where his left fist is, gravity is acting on A's barycenter C. If he weighs 100 kg on C is applied a force of 980 N which produces a torque like in a pendulum, right?. If θ = 45°, the actual $F_t$ acting on A will be 693 N in the tangential direction to C, at 45° with the ground.

I called this the 'discharged' force which is 71% of the original force. That is wrong! right, what is the correct terminology or is all that completely wrong?

- The point P where his right foot rests (in the picture here the centre O) is the point of support, the fulcrum. When he's not pulling and only g is in play, what is the force acting on P? Is parallelogram again useful here? if it is
then $F_p$ is = F * (siθ=cosθ), if he is pulling/leaning on the rope then $F_p$ should be equal to F (I said 100)%

Is this all completely wrong?

 

[CWatters]

Sorry for delay in replying. I'm in the UK.

The diagram is great but vanishes when I quote. Can you place one somewhere on the web so that I can pick it up?

http://i586.photobucket.com/albums/ss303/CWattersUK/TruckpullTorque.png

There is something I still do not understand:
there is no horizontal force on the ground in this sketch

I summed the torques about the mans feet. Torque = force * distance but the force you refer to is at the feet so the distance is zero. Likewise there is no vertical force shown at the mans feet.

if the man's weight is 100 kg , then the force of g is 1000N right? so the force of 300N is unrealistic? any ideas what pulling force a strong man of 100Kg can exert?

Consider what happens if the rope is attached to the man's centre of mass so that h_r = h_m= h and then he leans at 45 degrees.

Let the Tension in rope be T.

The man isn't accelerating/rotating so the torques sum to zero..

mg*h*cos(45) + T*sin(45) = 0

Solve for T

T = -mg*h*cos(45)/sin(45)

cos(45) = sin(45) so that cancels

T = -mgh which could easily be 1000n if the man weighs 100kg

Note: This explains why it's best for the man to hold the rope low down close to the ground. Perhaps even below his centre of mass. You get the leverage effect of h_m/h_r if they are different.

why can't he stand at 45° as long as the truck doesn't move??

He can but the tension in the rope might not be 300N.

 

[bobie]

Sorry for delay in replying. I'm in the UK.
http://i586.photobucket.com/albums/ss303/CWattersUK/TruckpullTorque.png
.

That's great!

I'll read the text and reply anon, in the meanwhile

could you be so kind as to scale it down a little and modify it putting the rope along the CoM (man's CoM is roughly at the sternum so they should coincide in a normall pull) and add the values for g 1000N (it's rougly 100 kg) have you read my answer to dalespam? isn't it necessary to draw the circle along which is applied the torque by g?

If it is not complicated can you tell me what program you used and if I can use it free? I am just a student.

 

[CWatters]

I used Paint.net which is free.

 

[CWatters]

That is interesting. There must be some extra degree of freedom then, because otherwise the system is overdetermined.

Consider this statement..

If a "ideal man" stands perfectly upright then it's not possible for him to exert any force on the rope.

By ideal man I mean one with feet of zero length so that his centre of mass is directly above his point of contact with the ground.

In this situation there is nothing to balance the torque produced by the rope. He mustlean back, or do something similar such as putting one foot behind the other which amounts to the same thing. Otherwise even the slightest tension in the rope would pull him over.

In short, even if there is sufficient friction with the ground, the limit to how much force he can apply on the rope is controlled by his mass and the geometry.

Aside: Find a strong man and have him stand with his heels and back to a wall. Tell him he can't move his feet. A skinny kid could pull him over easily as the man cannot get his centre of mass more than about a foot behind his point of contact with the ground.

 

[bobie]

, or do something similar such as putting one foot behind the other which amounts to the same thing. Otherwise even the slightest tension in the rope would pull him over..

Sure, but when CoM is beween the feet gravity exerts no torque and all its force is applied to the ground and is to no avail, like in the picture I posted, there the rope is about the height of center of mass (sternum) which is inside the base of the feet. he cannot exploit gravity.

 

[CWatters]

That's not correct. He can "exploit gravity" right up to the point where all his weight is on his front foot.

Consider what happens if something pulls on the rope with increasing force. At some point the man starts to rotate about the front foot and his rear foot just lifts off the ground. That sets a limit on how much force he/it can apply. eg how much he can exploit gravity. All the while his centre of mass is between his feet.

 

[CWatters]

If he has both feet on the ground (as per your clipart) then that complicates how you account for all the torques when you sum them to zero, but the approach and method is this same. The torques must still sum to zero if he isn't falling (eg if he's not subject to rotational acceleration).

[STRIKE]All you need to do is add an extra term for the weight on the back foot multiplied by the distance between his feet.[/STRIKE] The vertical force on the front foot can be ignored as that's the point about which you are summing the torques.

Edit: Actually it's not quite as simple as I implied in the strike out, but I'm running out of energy trying to explain it. Sorry.

 

[bobie]

That's not correct. He can "exploit gravity" right up to the point where all his weight is on his front foot.

Consider what happens if something pulls on the rope with increasing force. At some point the man starts to rotate about the front foot and his rear foot just lifts off the ground. That sets a limit on how much force he/it can apply. eg how much he can exploit gravity. All the while his centre of mass is between his feet.

I can't visualize it, I thought that he feels a pull only when CM is behind the base. What about the torque about the circle? if g 1s 1000N is it 710? can you draw it?

 

[CWatters]

I can't visualize it, I thought that he feels a pull only when CM is behind the base.

The CM has to be behind the point of rotation not the "base".

Sorry but I've got to go do other stuff for awhile.

 

[bobie]

He can but the tension in the rope might not be 300N.

Let me try:
if CM is at distance h (1m) from point P (fulcrum) and the rope is at that height

the torque of g is 100kg*1m*9.8* 0.7 = 693 n , so in order to balance the pull must exert 980n, which multiplied by 0.7 gives 693. But if bends slightly forward he can exert 300n without problems, is that right?

Now if g did not exist , or we consider only the pull, what force is applied to P on the ground 300n or 300/.7?

 

[jbriggs444]

Let me try:
if CM is at distance h (1m) from point P (fulcrum) and the rope is at that height

So the CM is 1 meter away from the fulcrum at an angle of 45 degrees above the horizontal. That is, it is about 0.7 meters back and 0.7 meters up, right? And the rope is at 1 meter height above the fulcrum.

EDIT: This appears to be a language difficulty. By "that height" you apparently meant "the height of the CM", not "1 meter". The intent is that the rope is about 0.7 meters above ground.

the torque of g is 100kg*1m*9.8* 0.7 = 693 n

693 Newton-meters. A torque is not a force. It has different units than a force.

so in order to balance the pull must exert 980n, which multiplied by 0.7 gives 693

Why are you multiplying by 0.7? The pull is 980 Newtons. The associated torque is 980 Newton-meters. Remember you put the rope 1 meter above the fulcrum, not 70 centimeters.

Edit: With the language issue corrected, the torque from the rope is indeed 693 Newton-meters.

But if bends slightly forward he can exert 300n without problems, is that right?

Not sure what you are trying to say here.

Edit: So by bending forward, the center of mass is imagined to move forward and up and the rope height is increased accordingly. Yes, if he leans forward far enough a torque of 300 Newtons times vertical distance from rope to fulcrum can balance a torque of 980 Newtons times horizontal distance from CG to fulcrum.

Now if g did not exist , or we consider only the pull, what force is applied to P on the ground 300n or 300/.7?

Are we still assuming that an equilibrium exists? If so, it is an impossible situation.

Edit: You are attempting to ask about the horizontal component of the force P applied on the ground. That's 300 Newtons. Conservation of momentum assures us of this.

 

[bobie]

So the CM is 1 meter away from the fulcrum at an angle of 45 degrees above the horizontal. That is, it is about 0.7 meters back and 0.7 meters up, right? And the rope is at 1 meter height above the fulcrum.
Why are you multiplying by 0.7? The pull is 980 Newtons. The associated torque is 980 Newton-meters. Remember you put the rope 1 meter above the fulcrum, not 70 centimeters.
Not sure what you are trying to say here.

Edit: So by bending forward, the center of mass is imagined to move forward and up and the rope height is increased accordingly. Yes, if he leans forward far enough a torque of 300 Newtons times vertical distance from rope to fulcrum can balance a torque of 980 Newtons times horizontal distance from CG to fulcrum.


Are we still assuming that an equilibrium exists? If so, it is an impossible situation.

Edit: You are attempting to ask about the horizontal component of the force P applied on the ground. That's 300 Newtons. Conservation of momentum assures us of this.

P is the point on the ground where are the feet: the fulcrum, right?
I wrote 1m distance from P (hm=h), as angle is 45° the height from the ground is .7m, right?
I am multiplying because the diagram says hmcosθ, which is .7, right. But I think the pull is not horizontal, as in the diagram, but tangential at hm, like in a pendulum, I got no reply to this.

I am not asking about the horizontal but the force of the pull acting from hm toward P at 45%, I said 300*cosθ, and was corrected to 300/cosθ, what is true and why? If I pull horizontally and prop up at 45° I thought the force is applied at 45° on the ground, than its horizontal component would be 300*cosθ

Thanks a lot

 

[A.T.]

But I think the pull is not horizontal, as in the diagram,

You are already confused by the geometry of this, and now you want to make it even more complicated, by introducing a non-horizontal rope?

 

[bobie]

You are already confused by the geometry of this, and now you want to make it even more complicated, by introducing a non-horizontal rope?

I was talking about the torque by g, isn't it like in a pendulum, tangential?

 

[sophiecentaur]

Thanks for your explanations, before I understand that I need to clarify what is probably misleading me:
1) isn't impulse a force? (I thought the only difference is that a force acts indefinitely and an impulse a short time) if that it is true can we substitute one with other?

2) I can't quote CWatter's picture, I can't yet post a diagram, so look at this:


- Roughly where his left fist is, gravity is acting on A's barycenter C. If he weighs 100 kg on C is applied a force of 980 N which produces a torque like in a pendulum, right?. If θ = 45°, the actual $F_t$ acting on A will be 693 N in the tangential direction to C, at 45° with the ground.

I called this the 'discharged' force which is 71% of the original force. That is wrong! right, what is the correct terminology or is all that completely wrong?



- The point P where his right foot rests (in the picture here the centre O) is the point of support, the fulcrum. When he's not pulling and only g is in play, what is the force acting on P? Is parallelogram again useful here? if it is
then $F_p$ is = F * (siθ=cosθ), if he is pulling/leaning on the rope then $F_p$ should be equal to F (I said 100)%

Is this all completely wrong?

It strikes me that you are not approaching this problem in the spirit, likely to help you in the long run. You need to start with the very basics of what was called 'statics' when I was at School. The basic definitions and the (simple) equations involved (involving basic Trig) with this sort of problem will always give you the right answer. If you don't do this 'right' then you cannot be sure of any conclusions you may come to because your predictions will not be bomb-proof. There is no quick fix for this sort of topic.

 

[Dale]

I see that there have been a bunch of replies, so some of this may be redundant.

1) isn't impulse a force? (I thought the only difference is that a force acts indefinitely and an impulse a short time) if that it is true can we substitute one with other?

No. Impulse is force times time, or more specifically the integral of force with respect to time. Impulse does not need to be a short time, but often in collision you are interested in forces which have a finite impulse over a very short time and don't care about the actual force. Impulse has units of momentum, it is definitely not force.

- Roughly where his left fist is, gravity is acting on A's barycenter C. If he weighs 100 kg on C is applied a force of 980 N which produces a torque like in a pendulum, right?. If θ = 45°, the actual $F_t$ acting on A will be 693 N in the tangential direction to C, at 45° with the ground.

I called this the 'discharged' force which is 71% of the original force. That is wrong! right, what is the correct terminology or is all that completely wrong?

Just call it an "exerted" force or an "applied" force. The percentage of the original force is irrelevant, since there is no conservation of force and therefore may not be any 29% force.

- The point P where his right foot rests (in the picture here the centre O) is the point of support, the fulcrum. When he's not pulling and only g is in play, what is the force acting on P? Is parallelogram again useful here? if it is
then $F_p$ is = F * (siθ=cosθ), if he is pulling/leaning on the rope then $F_p$ should be equal to F (I said 100)%

Is this all completely wrong?

I don't know, I would have to work out the forces but I cannot do that now. Yes, the parallelogram rule and all of the other standard rules of vector addition are important here. The fundamental relationship is Newton's laws, especially his 2nd law.

Personally, I would recommend simplifying the secenario and not worrying about torques. Consider a one-legged man so that you can have a single force on the ground, and consider both the force on the ground and the tension from the rope to be acting in line with the center of mass so that there is no torque, and consider the tension to be horizontal. Thus you have only 3 forces (horizontal tension (T), vertical weight (mg), and ground reaction (R) at an angle of theta with the ground) and 0 torques.

Do you know how to solve this simplified problem?

 

[CWatters]

Let me try:
if CM is at distance h (1m) from point P (fulcrum) and the rope is at that height.
[the torque of g is 100kg*1m*9.8* 0.7 = 693 n , so in order to balance the pull must exert 980N, which multiplied by 0.7 gives 693NM.

I believe this is correct!

Assumptions:

The 1m is measured along his body.
He's leaning at 45 degrees.

So the torque equation is...

m*g*h*cos(45) + T*h*sin(45) = 0

h cancels
cos(45) = sin(45) = 0.7 so that also cancels

gives

m*g + T = 0

T = -mg = 980 NM

But if bends slightly forward he can exert 300n without problems, is that right?

Correct. If he doesn't lean at 45 degrees he will exert a lower force on the rope.

... what force is applied to P on the ground 300n or 300/.7?

Ok to answer the last part of that you have to look at the diagram showing the horizontal forces.

If the man is not accelerating then the horizontal forces must sum to zero. The only two horizontal forces acting on the man are:

The tension in the rope T = 300N
The friction force with the ground (call it Fgnd).

So..

T + Fgnd = 0

or

Fgng = -T

If T = 300N then Fgnd = -300N

The negative sign is because they are in opposite directions.

Edit: Note this is just the horizontal force the man applies to the ground not the total force he applies to the ground. If you want to work out that you have to calculate the angle that he has to lean at to generate 300N instead of 980N

 

[bobie]

Ok to answer the last part of that you have to look at the diagram showing the horizontal forces.
If the man is not accelerating then the horizontal forces must sum to zero. The only two horizontal forces acting on the man are:
The tension in the rope T = 300N
The friction force with the ground (call it Fgnd)
T + Fgnd = 0
Fgng = -T
If T = 300N then Fgnd = -300N
The negative sign is because they are in opposite directions.
Edit: Note this is just the horizontal force the man applies to the ground not the total force he applies to the ground. If you want to work out that you have to calculate the angle that he has to lean at to generate 300N instead of 980N

I do not follow you, he is exerting F =300 N, so the maximum force on the ground cannot exceed that value. You are saying, if I got it right, that all the force is deviated horizontally? there is no vertical component? is that possible?
I made a sketch according to the pallalelogram rule, (gravity exerts no torque and is fully applied to the ground):
http://s47.photobucket.com/user/lisa0rg/media/PullT_zps6c8c5be2.jpg.html?filters[user]=141333040&filters[recent]=1&sort=1&o=0
http://s47.photobucket.com/user/lisa0rg/media/PullT_zps6c8c5be2.jpg.html?filters[user]=141333040&filters[recent]=1&sort=1&o=0
I don't know why the image doesn't show properly, click on the link ,
but anyway are forces wrong?


Thanks a lot for your suggestion paint.net is great!

 

[A.T.]

I do not follow you, he is exerting F =300 N, so the maximum force on the ground cannot exceed that value.

If he is in equilibrium all horizontal forces on him must balance. If the rope pulls him at 300N to the left, then the ground pushes him at 300N to the right. Sum of horizontal forces on him is zero.

You are saying, if I got it righr, that all the force is deviated horizontally? there is no vertical component?

Sure there is a vertical component of the ground reaction force. In equilibrium something must balance his weight. If his weight is 1000N down, then the vertical ground reaction is 1000N up. Sum of vertical forces on him is zero.

 

[bobie]

If he is in equilibrium all horizontal forces on him must balance. If the rope pulls him at 300N to the left, then the ground pushes him at 300N to the right. Sum of horizontal forces on him is zero.

Sure there is a vertical component of the ground reaction force. In equilibrium something must balance his weight. If his weight is 1000N down, then the vertical ground reaction is 1000N up. Sum of vertical forces on him is zero.

- No I am not talking of reaction, AT, the reaction of course will be equal and contrary, but the ground can cope with any force, that is not the problem, but
if you exert a F at an angle , F becomes F cos y. Resolution-of-Forces Is it always valid or not? if he is pushing on the ground at 45° must there not be an x and a y component? how can the whole force go un the x axis?, according to my sketch, btw can you make it visible?, the ground is reacting to 980 N (G) and 210 N (push from rope) , for a total 1190N where is the problem. The ground is reacting horizontally to his right foot with a force of 210N (stiction)

Forces are not always in equilibrium, when the truck moves it means that the reaction is <299N, right?

 

[A.T.]

210 N (push from rope)

Rope tension is 300N in your diagram.

Forces are not always in equilibrium, when the truck moves it means that the reaction is <299N, right?

If it moves at constant speed the forces are in equilibrium. If it accelerates then you are likely accelerating too, so the ground force on you greater than the rope force on you.

 

[bobie]

Rope tension is 300N in your diagram.
.

Yes rope tension is 300N on the truck and the right foot, and on the ground it becomes 210 x-axis and 210 x-axis
what is wrong?

 

[A.T.]

Yes rope tension is 300N on the truck and the right foot, and on the ground it becomes 210 x-axis and 210 x-axis
what is wrong?

You are losing against the truck, and accelerating towards it.

 

[bobie]

You are losing against the truck, and accelerating towards it.

No, the forces balance,
here: http://s47.photobucket.com/user/lisa0rg/media/PullT_zps6c8c5be2.jpg.html?filters[user]=141333040&filters[recent]=1&sort=1&o=0
The truck is budging

http://s47.photobucket.com/user/lisa0rg/media/PullT_zps6c8c5be2.jpg.html?filters[user]=141333040&filters[recent]=1&sort=1&o=0
Thanks, anyway, I'll see for what dalespam says (tonight) of the reason why the parallelogram must not be applied here, or tomorrow for CWatters

 

[A.T.]

No, the forces balance,

No they don't. The friction of 210N is not sufficient to balance the opposed 300N rope pull.

The truck is budging

Not only budging, but plowing the field with you.

why the parallelogram must not be applied here, or tomorrow for CWatters

CWatters explained to you how to apply the parallelogram on page 2:
https://www.physicsforums.com/showpost.php?p=4840187&postcount=29

 

[bobie]

CWatters explained to you how to apply the parallelogram on page 2:
https://www.physicsforums.com/showpost.php?p=4840187&postcount=29

If the force on right foot is 424N, that means that the forces on x and y-axis sum up to 424*cos 45 * 2 = 600N.
You are doubling the force applied by the man, that seems rather unrealistic.
The forces in the sketch are perfectly balanced as the big red arrows show, so 3rd law is respected , and also 2nd law , because the reaction of the truck is slaller and the truck gives way a few cm and the rope is accelerating.

 

[A.T.]

If the force on right foot is 424N, that means that the forces on x and y-axis sum up to 424*cos 45 * 2 = 600N.

Adding x to y components is meaningless nonsense. This is not how vector addition works.

The forces in the sketch are perfectly balanced

Nope. All the x-components must add to zero. But they don't.

 

[bobie]

Adding x to y components is meaningless nonsense. This is not how vector addition works.
Nope. All the x-components must add to zero. But they don't.

Have you looked at the sketch? can you make it visible in your post?
the y and x components match perfectly 210 -210, 300 -300, if 300 -290, they do not match and the puller won his trophy.

Be kind and give me a couple of links where to learn how to add vectors
These are not good:
Resolution-of-Forces
http://www.physicsclassroom.com/class/vectors/Lesson-3/Resolution-of-Forces

http://www.physicsclassroom.com/class/vectors/Lesson-3/Resolution-of-Forces
Vector-Addition
http://mathworld.wolfram.com/VectorAddition.html
vector

 

[A.T.]

the y and x components match perfectly

Nope. The x components of the forces acting on the man do not add up to zero.

F_rope + F_friction = -300N + 210N = -90N ≠ 0

 

[Dale]

Thanks, anyway, I'll see for what dalespam says (tonight) of the reason why the parallelogram must not be applied here

Sorry, there has been a lot of conversation. I am not sure what it is that you would like me to respond to.

 

[bobie]

Sorry, there has been a lot of conversation. I am not sure what it is that you would like me to respond to.

Please say a final word on the value of the pull force on the left foot and on th x and y-axis and the use of parallelogram.
Pull on rope/truck
http://s47.photobucket.com/user/lisa0rg/media/PullT_zps6c8c5be2.jpg.html?filters[user]=141333040&filters[recent]=1&sort=1&o=0

I think that will end the controversy. I'll start a thread on impulse / force if you want to clarify those concept.
Thanks Dalespam, you are exquisite as ever

 

[A.T.]

I'll start a thread on impulse / force if you want to clarify those concept.

You should make yourself familiar with the concept of vectors. I don't see how you can even claim that the forces in your diagram balance, without understanding how forces are added.

 

[bobie]

Nope. The x components of the forces acting on the man do not add up to zero.

F_rope + F_friction = -300N + 210N = -90N ≠ 0

Where did you get those numbers?
firction is 210 equal to Px component -210
pull of rope is 300 equal to -300 reaction of truck (stiction + inertia); when they do not match you have + 300 -299, ... -290 = +1...+10 and the track has moved

 

[A.T.]

Nope. The x components of the forces acting on the man do not add up to zero.

F_rope + F_friction = -300N + 210N = -90N ≠ 0

Where did you get those numbers?

Read again.

firction is 210 equal to Px component -210
pull of rope is 300 equal to -300 reaction of truck

It makes no sense to add 3rd Law paired forces, which act on different object each. You have to add all the forces acting on a single object: the man.

 

[bobie]

Read again.


It makes no sense to add 3rd Law paired forces, which act on different object each. You have to add all the forces acting on a single object: the man.

Who says that? reference please!
That does not make sense as the three reactions act all on the man whereas his actions are exertted on three different obiects.

 

[Dale]

Please say a final word on the value of the pull force on the left foot and on th x and y-axis and the use of parallelogram.

The diagram is pretty cluttered. When you do a true free-body diagram one of the important rules is to only draw the forces acting ON the free-body. If you have multiple objects that you want to analyze then you draw a separate free-body diagram for each object and on each diagram place only the forces acting ON that object. Specifically, on this diagram you should not include the force of the leg on the ground, only the force of the ground on the leg. Also, you should not include the force of the arm on the rope, but only the force of the rope on the arm.

If you delete all of the forces acting on other objects then you are left with the attached drawing. Note how it is much clearer to analyze this diagram than the previous one. By removing the clutter you immediately see the following:

1) The vertical forces do balance out, meaning that the person is not sinking into the ground or jumping off the ground.

2) The horizontal forces do not balance out, meaning that the person is being accelerated towards the truck at a rate of (290-210) N/ 100 kg = .8 m/s². Either the rope tension must be less or the friction force must be greater for the person to not accelerate.

3) The force on the front leg is purely horizontal, which is probably not what was intended. I suspect that you want the force on the front leg to be at a 45° angle, but that is not what is drawn here.

 

[Dale]

Who says that? reference please!

A.T. is correct. If he does not post a reference then I am sure I can dig up several.

 

[bobie]

1) The vertical forces do balance out, meaning that the person is not sinking into the ground or jumping off the ground.

2) The horizontal forces do not balance out, meaning that the person is being accelerated towards the truck at a rate of (290-210) N/ 100 kg = .8 m/s². Either the rope tension must be less or the friction force must be greater for the person to not accelerate.

3) The force on the front leg is purely horizontal, which is probably not what was intended. I suspect that you want the force on the front leg to be at a 45° angle, but that is not what is drawn here.

Thanks, Dalespam
3) the force at 45° was in blue in the drawing 300N that has been split by the parallelogram. Is that procedure wrong (can I say 'split'?).
Now, the force any man can pull is easily measured (by instruments maybe, or ) in a simple way adding a couple of pulleys ans checking what is the maximum F. Suppose it is 2000N (is it a plausible figure) we'll make him do his outmost and consider that value.
If he is pulling 2000N the force on his foot (we excluded g, but we might solve the problem in this way shifting the CM so that on the right foot there is an extra F = 90).
But I am not looking for a cheap solution. I want to understand how you justify that exerted F is 2000 and on the foot becomes 2800. Can you suggest me a **formula to calculate how g is distributed between the two legs?

2) The reaction of the truck is nominal. If he were in a tug of war then 300N would be effective. Here we are dealing with passive resistance by stiction and inertia, the reaction immediately varies / adjusts itself with the action doesn't it? if it doesn't the man instinctively bend forward shifting (discharging) its weight on the fore leg, right?

Thanks
**do you think such formula exists?

P.S. Why I cannot upload my image from the web?

 

[Dale]

Thanks, Dalespam
3) the force at 45° was in blue in the drawing 300N that has been split by the parallelogram. Is that procedure wrong (can I say 'split'?).

That was the force on the ground FROM the leg, not the force from the ground ON the leg. Remember, in a free-body diagram we only include the forces that are acting ON our free body, not the forces FROM our free body which are acting on other objects. So, this should have been drawn as a 300 N force at 45° upwards acting on the leg.

Splitting the force into components is fine, but it just does not belong on this free-body diagram.

Can you suggest me a **formula to calculate how g is distributed between the two legs?

Yes, if the man is in static equilibrium then:
$\Sigma f=0$ and $\Sigma \tau = 0$.

2) The reaction of the truck is nominal. If he were in a tug of war then 300N would be effective. Here we are dealing with passive resistance by stiction and inertia, the reaction immediately varies / adjusts itself with the action doesn't it? if it doesn't the man instinctively bend forward shifting (discharging) its weight on the fore leg, right?

Whatever the force ON the man is, that is what you put on a free-body diagram. If the magnitude of that force is unknown then simply assign it a variable name (like "T") and then solve for its value. Whether the force is "passive resistance" or whatever else is not important.

For this scenario, if we have that the mass of the weight is 980 N and if we are given that the force on the front leg is 300 N at an angle of 45° upwards then the force on the other leg is 768 N upwards, and the tension in the rope is 212 N horizontal (assuming equilibrium).

 

[A.T.]

Who says that? reference please!

I gave you one on page 2 already. Did you read it?
https://www.physicsforums.com/showpost.php?p=4840189&postcount=30

That does not make sense as the three reactions act all on the man whereas his actions are exertted on three different obiects.

The terms "action" and "reaction" in the context of the 3rd law are assigned arbitrarily, and are interchangeable.

 

[CWatters]

You are saying, if I got it right, that all the force is deviated horizontally? there is no vertical component?

No, I meant that I had only calculated the horizontal component. You can calculate the vertical component by looking at the vertical forces (which also sum to zero).

To work out the total force at the mans feet you need to add (vector add) the horizontal and vertical components.

 

[bobie]

No, I meant that I had only calculated the horizontal component. You can calculate the vertical component by looking at the vertical forces (which also sum to zero).

To work out the total force at the mans feet you need to add (vector add) the horizontal and vertical components.

Hi CWatters, I have corrected my sketch:
ManPullsT
http://s47.photobucket.com/user/lisa0rg/media/ManPullsT_zps61720dbc.jpg.html
Can you tell me if it is OK?
I am not sure if all forces on the body must be negative, as usually g is considered negative and the reaction positive. Shall I use + and - according to the axis x, an what about the forces at 45, which are minus?
Can you tell me hou to calculate the remaining g on the left leg as here I cannot use the parallelogram.

THanks again, you have been very kind to suggest paint.net and I used also your bucket shop.
Can you tell me why your image is stand alone and mine has all the ads etc?

 

[A.T.]

Hi CWatters, I have corrected my sketch: Can you tell me if it is OK?

It's incomprehensible. What are those G124, G88, R212? Make a legend defining the names. Why don't you take DaleSpam's advice and draw only the external forces acting on the man? There are only three of them. Spohiecentraur did that diagram for you on page 1, with just one small error (direction of ground reaction).

 

[Dale]

Hi CWatters, I have corrected my sketch:
ManPullsT
http://s47.photobucket.com/user/lisa0rg/media/ManPullsT_zps61720dbc.jpg.html
Can you tell me if it is OK?

None of the blue forces should be on this diagram. Also, gravity, by definition, has no horizontal component, so I don't know why you have the extra green arrows. Finally, on the red arrows at the front foot it is unclear if you are intending to break the 45° reaction force into components. If so then where is the vertical component, if not then why is there a horizontal component?

 

[bobie]

None of the blue forces should be on this diagram. Also, gravity, by definition, has no horizontal component, so I don't know why you have the extra green arrows. Finally, on the red arrows at the front foot it is unclear if you are intending to break the 45° reaction force into components. If so then where is the vertical component, if not then why is there a horizontal component?

The vertical component was missing it is -88 N. I'll post a new corrected diagram probably before you get back to this post.
The blue forces are in the diagram just for you to check if is at last correct.

As to gravity when you put yor legs astride (trying to do a split) when the angle exceeds 45° the weight is distributed on each leg and the dorce is 'split' /divided in 2 normal components, if the floor is waxed you slip and may dislocate your femur /hip. Moreover the blu force on the front foot cannot exceed 300N and the missing 124 N (if you want to get an x-force 300N) can come only from g.

** here is the image Pull-complete

 

[CWatters]

Can I persuade you to show that the horizontal, vertical and torques each sum to zero. That way you/we can see if it's all consistent.

For example do the vertical components of the forces acting on each foot add up to 980N?