3D Visualization of Temperature Distribution Function

[fluidistic]

I just downloaded scilab because Wolfram Alpha wouldn't want to plot the function I'd like.
In a physics problem I've found the temperature distribution of a 2 dimensional system. I'd like to visualize this function in 3d.
The function I want to plot is u(x,y)=\frac{1}{\pi} \arctan \left ( \frac{y+a}{x} \right )+\frac{1}{\pi} \arctan \left ( \frac{a-y}{x} \right ). I've read the help file of scilab of how to plot but I'm getting lost very quickly. Any help is appreciated!

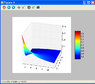
Edit: so far I have

x=[0:0.1:12]'; y=[0:0.1:12]'; z=atan((y-2)/x)+atan((2-y)/2); plot3d(x,y,z)

. I don't know how to pass a line (enter just evaluates the command I wrote). I get the message "Inconsistent addition."

 

[gsal]

Don't know scilab, but your second 'atan' has a '2' in the denominator...shouldn't that be 'x'?

what do the single apostrophes do?
what do you think you are accomplishing with z=... ? are x and y traversed independently as if they were in 2 nested do-loops...or is it just a one-to-one? In other words, is z also just a vector? or are you getting a matrix?

try to input one line at a time and find out what you get back after each...don't jump all the way to plotting...baby steps, baby steps!

 

[fluidistic]

Don't know scilab, but your second 'atan' has a '2' in the denominator...shouldn't that be 'x'?

No problem. Yes, it should be an x.

what do the single apostrophes do?

I have absolutely no idea. Probably a necessary part of syntax.

what do you think you are accomplishing with z=... ? are x and y traversed independently as if they were in 2 nested do-loops...or is it just a one-to-one? In other words, is z also just a vector? or are you getting a matrix?

Hmm, I wanted it to be a function of both x and y and then plot it. My u(x,y)

try to input one line at a time and find out what you get back after each...don't jump all the way to plotting...baby steps, baby steps!

Ok.
Here is an example they give, from which I've been inspired:

// simple plot using z=f(x,y) 
t=[0:0.3:2*%pi]';
z=sin(t)*cos(t');
plot3d(t,t,z)

Edit: It seems that x=[0:0.1:12] is a matrix or so. I thought it would plot x from 0 to 12 with increment of 0.1. Sigh. I really have no idea about Scilab.

 

[gsal]

ok, so, did the example work? Did you get a surface plot?

I think the apostrophe means transpose. In the example where they multiply sin times cos, notice how they pass t to one function and t' to the other...the fact that these two vectors are orthogonal (one is a column vector and the other a row vector) may be what makes it produce a square matrix for z...in other words, the expression is evaluated as in a double loop.

So, go back to your own problem and pass y and x' and see what you get...see if you can display the z matrix before plotting to see if in fact is a square matrix.

 

[Dr Transport]

look at the function meshgrid if it exists in scilab (it is a MATLAB function), you need a 2-d grid to properly plot in 3-d

 

[fluidistic]

ok, so, did the example work? Did you get a surface plot?

I think the apostrophe means transpose. In the example where they multiply sin times cos, notice how they pass t to one function and t' to the other...the fact that these two vectors are orthogonal (one is a column vector and the other a row vector) may be what makes it produce a square matrix for z...in other words, the expression is evaluated as in a double loop.

So, go back to your own problem and pass y and x' and see what you get...see if you can display the z matrix before plotting to see if in fact is a square matrix.

I tried:

-->x=[0:0.1:12]';
 
-->y=[0:0.1:12]';
 
-->z=atan((y-2)/x)+atan((2-y)/x);
 
-->plot3d(x,y,z)

I do get a 3d surface but it's all flat.

 

[fluidistic]

In analogy to their working example:

x = -1:0.1:1;
y = -1:0.1:1;

[X,Y] = meshgrid(x,y);

for i=1:size(X,1)
  for j=1:size(X,2)
    Z(i,j) = sinc(2*%pi*X(i,j)*Y(i,j));
  end
end

surf(X,Y,Z)

I do:

-->x = 1:0.1:12;
 
-->y = 1:0.1:12;
 
-->
 
-->[X,Y] = meshgrid(x,y);
 
-->
 
-->for i=1:size(X,1)
-->  for j=1:size(X,2)
-->    Z(i,j) = atan((Y(i,j)-2)/X(i,j))+atan((2-Y(i,j))/X(i,j));
-->  end
-->end
 
-->
 
-->surf(X,Y,Z)

And I still get a totally planar surface.

 

[gsal]

I think the reason you are getting a flat surface is because you have yet another typo which effectively makes the summation be zero...

in your numerators, you have Y-2 and 2-Y ...you should have Y+2 and 2-Y

and, for completeness, you may want to put back the division by PI

 

[fluidistic]

I think the reason you are getting a flat surface is because you have yet another typo which effectively makes the summation be zero...

in your numerators, you have Y-2 and 2-Y ...you should have Y+2 and 2-Y

and, for completeness, you may want to put back the division by PI

Whoops you're right. Well since I took a=2 while it's totally arbitrary, I don't think the 1/pi factor is really relevant.
Using the meshgrid I get a somehow decent surface, but doesn't work well for the plot3d command so far.
Here are 2 screenshots.

 

[gsal]

Hhhmm...here it is what it looks like with python and matplotlib.

 

[fluidistic]

Hhhmm...here it is what it looks like with python and matplotlib.

Maybe it's the same. If you take a=2, I suggest you to reduce the box up to y and x=6 rather than 12.