-11.2 IVP in explicit form.

[karush]

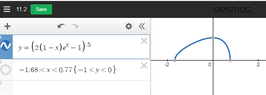
View attachment 9112

Given #11
$\quad\displaystyle
xdx+ye^{-x}dy=0,\quad y(0)=1$
a. Initial value problem in explicit form.
$\quad xdx=-ye^{-x}dy$
separate
$\quad \frac{x}{e^{-x}}\, dx=-y\, dy$
simplify
$\quad xe^x\, dx=-y\, dy$
rewrite
$\quad y\,dy=-xe^x\,dx$
integrate (with boundaries)
$\quad \int_1^y u\,dy=-\int_0^x ve^v\,dv$

OK i did this so far hopefully ok but didnt know how to do b and c (on desmos)

b. Plot the graph of the solution
c. Interval of solution.

 

[cbarker1]

Re: 11.2

I recommend that you integrate both side to find the curve and the graph as well as provide that answer to us.

 

[HallsofIvy]

Re: 11.2

(You have a typo- your "dy" should be "du".)

Why stop there? Obviously you have to do the integrals! The "du" integral is straight forward. To do the "dv" integral, use "integration by parts".

Solving for y will involve a square root. The domain is determined by the fact that the square root must be of a non-negative number. The graph will have two parts, one with "+", the other with "-".

 

[MarkFL]

Re: 11.2

What title would you like me to give this thread so that the title is useful?

 

[karush]

Re: 11.2

11.2 Initial value problem in explicit form.

I tried to fix it but couldn't

==================================

integrate (with boundaries)
$$\int_1^y y\,dy=-\int_0^x xe^x\,dx$$
then
$\frac{y^2}{2}-\frac{1}{2}=-e^xx+e^x-1$
isolate y
multiply thru by 2 and add 1
$y^2=-2e^xx+2e^x-2+1$
simplify RHS and factor
$y^2=2[1-x]e^x-1$
square both sides
$y = 2[(1-x)e^x-1]^{1/2}$

typo maybe??

when this is graphed you get nothing?

 

[topsquark]

Re: 11.2

thake the square (root) of both sides
$y = 2[(1-x)e^x-1]^{1/2}$

typo maybe??

when this is graphed you get nothing?

The "2" belongs under the square root. Typo? (Sun)

Here's the graph. I have no idea why this would cause you trouble.
View attachment 9113

And don't forget the part of the solution with the negative sign!

-Dan

 

[karush]

View attachment 9117
here is the desmos attemptalso I don't know where the interval of $−1.68<x<0.77$ which is the book answer comes from
I set y=0 but that didn't return those values

 

[HallsofIvy]

here is the desmos attemptalso I don't know where the interval of $−1.68<x<0.77$ which is the book answer comes from
I set y=0 but that didn't return those values

What values did you get? If I graph the function on Desmos (https://www.desmos.com/calculator) clicking on the y-intercept, I get x= -1.678 and x= 0.768)

If y= 0 then $$2(1- x)e^x- 1= 0$$ then $$2(1- x)e^x= 1$$.

Let u= 1- x so that x= 1- u. The equation becomes $$2ue^{1- u}= 2eue^{-u}= 1$$. Let v= -u so that u= -v. The equation becomes $$-2eve^v= 1$$. Divide both sides by -2e. $$ve^v= -\frac{1}{2e}$$. Then $$v= W\left(\frac{-1}{2e}\right)$$ where "W" is "Lambert's W function, defined as the inverse function to $$f(x)= xe^x$$.