karush
Gold Member
MHB
- 3,240
- 5
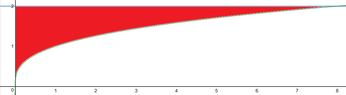
solve by reversing the reversing the order of integration
this was given:
\begin{align*}\displaystyle
I&=\int_0^8 \int_{\sqrt[3]{x}}^2
\left[\frac{x}{y^7+1}\right]dy \, dx\\
\end{align*}
ok I put this in an dbl int calculor but it turned the order around to
\begin{align*}\displaystyle
I&=\int_{\sqrt[3]{x}}^2 \int_0^8
\left[\frac{x}{y^7+1}\right]dy \, dx\\
\end{align*}
this was given:
\begin{align*}\displaystyle
I&=\int_0^8 \int_{\sqrt[3]{x}}^2
\left[\frac{x}{y^7+1}\right]dy \, dx\\
\end{align*}
ok I put this in an dbl int calculor but it turned the order around to
\begin{align*}\displaystyle
I&=\int_{\sqrt[3]{x}}^2 \int_0^8
\left[\frac{x}{y^7+1}\right]dy \, dx\\
\end{align*}