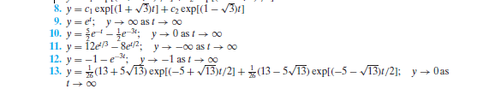karush
Gold Member
MHB
- 3,240
- 5
find the solution of the given initial value problem:
$6y''-5y'+y=0\quad y(0)=4 \quad y'(0)=0$
if $r=e^{5t}$ then
$\displaystyle 6y''-5y'+y=(r-3)(r-2)=0$
then
$y=c_1e^{3t}+c_1e^{2t}=0$
for $y(0)=4$
$y(0)=c_1e^{3(0)}+c_1e^{2(0)}=4$
ok I don't see how the last few steps lead to the book answer (11)
View attachment 9019
$6y''-5y'+y=0\quad y(0)=4 \quad y'(0)=0$
if $r=e^{5t}$ then
$\displaystyle 6y''-5y'+y=(r-3)(r-2)=0$
then
$y=c_1e^{3t}+c_1e^{2t}=0$
for $y(0)=4$
$y(0)=c_1e^{3(0)}+c_1e^{2(0)}=4$
ok I don't see how the last few steps lead to the book answer (11)
View attachment 9019