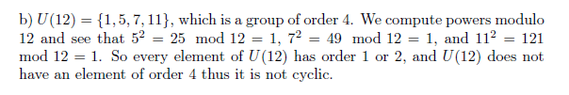3.13 Compute the orders of the following groups:

[karush]

\nmh{837}
Compute the orders of the following groups: $U(3), U(4), U(12)$ and $U(3), U(5), U(15)$.
On the basis of your answers, make a conjecture about the relationship among $|U(r)|, |U(s)|$, and $|U(rs)|$.

ok I still don't have a clear idea on how to do this $ax=1$
$U(3)=3$

 

[Chris L T521]

Compute the orders of the following groups: $U(3), U(4), U(12)$ and $U(3), U(5), U(15)$.
On the basis of your answers, make a conjecture about the relationship among $|U(r)|, |U(s)|$, and $|U(rs)|$.

ok I still don't have a clear idea on how to do this $ax=1$
$U(3)=3$

If I'm not mistaken, the order of $U(n)$ is $\varphi(n)$, which is the Euler's totient function. If $n$ is prime, then $\varphi(n) = n-1$. If $p$ is prime and $n=p^k$, then $\varphi(n) = p^{k-1}(p-1)$. Also, if $\gcd(m,n)=1$, $\varphi(mn) = \varphi(m)\varphi(n)$. Using these properties of $\varphi(n)$, you should be able to find the orders. I leave it to you to find the orders of the groups and make a conjecture about how $|U(rs)|$, $|U(r)|$ and $|U(s)|$ are related.

I hope this helps!

 

[karush]

View attachment 8397

ok I found this for u(12)
where does {1,5,7,11} come from? I see that 1+11=12 and 5+7=12
also "every element of U(12) has order of 1 or 2" where does 2 come from

also from this does it mean that
U(3)={1,2} and u(5)={1,4}

 

[karush]

https://dl.orangedox.com/GXEVNm73NxaGC9F7Cy