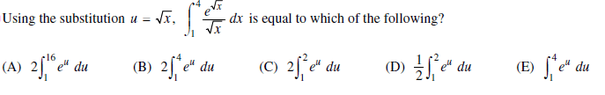SUMMARY
The discussion centers on the evaluation of the integral $\displaystyle2 \int _1^2 e^u \, du$ derived from the original integral $\displaystyle2 \int_1^4 \frac{e^{\sqrt{x}}}{2 \sqrt{x}} \, dx$. The variable substitution $u = \sqrt{x}$ necessitates a change in the limits of integration from $x = 1$ to $x = 4$ into $u = 1$ to $u = 2$. Participants clarify that when changing variables, all references must be updated accordingly, ensuring the correct limits are applied for accurate integration.
PREREQUISITES
- Understanding of integral calculus and variable substitution
- Familiarity with the exponential function and its properties
- Knowledge of limits of integration in definite integrals
- Ability to perform basic algebraic manipulations
NEXT STEPS
- Study the process of variable substitution in integrals
- Learn about the properties of the exponential function in calculus
- Explore the concept of changing limits of integration during substitution
- Practice solving definite integrals with various substitutions
USEFUL FOR
Students preparing for the AP Calculus exam, educators teaching integral calculus, and anyone seeking to improve their understanding of variable substitution in integration.