5.1.313 AP Calculus Exam DE on bird weight

[karush]

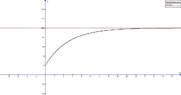
View attachment 9342
I just posted a image due to overleaf newcommands and graph

ok (a) if we use f(20) then the $B=0$ so their no weight gain.

(b), (c), was a little baffled and not sure how this graph was derived...

 

[skeeter]

(a) $\dfrac{dB}{dt} > 0$ for $20 \le B < 100$ ... what does that say about the change in the bird's weight?

(b) $\dfrac{d}{dt} \left[\dfrac{dB}{dt} = \dfrac{1}{5}(100-B) \right]$

$\dfrac{d^2B}{dt^2} = -\dfrac{1}{5}(100-B) < 0 \implies B(t) \text{ is concave down everywhere}$

(c) $\dfrac{-1}{100-B} \, dt = -\dfrac{1}{5} \, dt$

$\log|100-B| = -\dfrac{t}{5} + C$

$B(0) = 20 \implies C = \log(80)$

$100-B = 80e^{-t/5} \implies B = 100 - 80e^{-t/5}$

the function $B(t)$ is an example of inhibited exponential growth ... note $$\lim_{t \to \infty} B(t) = 100$$

 

[karush]

did you do the graph in tikx?

great help... appreciate all the steps

 

[skeeter]

did you do the graph in tikx?

no, I've had this free graphing program for quite a while ...

https://www.padowan.dk/

 

[HallsofIvy]

(a) $\dfrac{dB}{dt} > 0$ for $20 \le B < 100$ ... what does that say about the change in the bird's weight?

(b) $\dfrac{d}{dt} \left[\dfrac{dB}{dt} = \dfrac{1}{5}(100-B) \right]$
$\dfrac{d^2B}{dt^2} = -\dfrac{1}{5}(100-B) < 0 \implies B(t) \text{ is concave down everywhere}$

No, you didn't differentiate on the right side.
$\frac{d^2B}{dt^2}= \dfrac{d}{dt}[dfrac{1}{5}(100- B)= \dfrac{1}{5}(-B)=- \frac{1}{5}B$

(c) $\dfrac{-1}{100-B} \, dt = -\dfrac{1}{5} \, dt$

The left side should be $\dfrac{-1}{100- B}dB$. not "dt".

$\log|100-B| = -\dfrac{t}{5} + C$

$B(0) = 20 \implies C = \log(80)$

$100-B = 80e^{-t/5} \implies B = 100 - 80e^{-t/5}$

the function $B(t)$ is an example of inhibited exponential growth ... note $$\lim_{t \to \infty} B(t) = 100$$

 

[karush]

no, I've had this free graphing program for quite a while ...

https://www.padowan.dk/

looks pretty clean and basic... which is very nice..

 

[skeeter]

No, you didn't differentiate on the right side.
$\frac{d^2B}{dt^2}= \dfrac{d}{dt}[dfrac{1}{5}(100- B)= \dfrac{1}{5}(-B)=- \frac{1}{5}B$The left side should be $\dfrac{-1}{100- B}dB$. not "dt".

yep ... it happens.