6.1.1 AP Calculus Inverse of e^x

[karush]

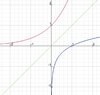
If $f^{-1}(x)$ is the inverse of $f(x)=e^{2x}$, then $f^{-1}(x)=$$a. \ln\dfrac{2}{x}$
$b. \ln \dfrac{x}{2}$
$c. \dfrac{1}{2}\ln x$
$d. \sqrt{\ln x}$
$e. \ln(2-x)$

ok, it looks slam dunk but also kinda ?

my initial step was
$y=e^x$ inverse $\displaystyle x=e^y$
isolate
$\ln{x} = y$

the overleaf pdf of this project is here ... lots of placeholders...

https://drive.google.com/open?id=1WyjkfLAzhs4qF3RYOgSJrllP4hoKC5d4

 

[skeeter]

The inverse of $f(x)=e^x$ is $f^{-1}(x) = \ln{x}$

... there is an obvious mistake in the answer choices.

Maybe a typo? $f(x) = e^{2x}$ ?

 

[karush]

[DESMOS]advanced: {"version":7,"graph":{"showGrid":false,"viewport":{"xmin":-6.972973201241764,"ymin":-5.621621669007776,"xmax":13.027026798758236,"ymax":6.733590697123048}},"expressions":{"list":[{"type":"expression","id":"graph1","color":"#2d70b3","latex":"f(x)=e^x"},{"type":"expression","id":"2","color":"#388c46","latex":"\\left(\\frac{1}{2}\\right)\\ln x"},{"type":"expression","id":"3","color":"#c74440","latex":"y=x","lineStyle":"DASHED"}]}}[/DESMOS]

well graphing it looks like its (c)

so how?

 

[skeeter]

the graph is close, but no cigar.

$f(1)=e \implies f^{-1}(e) =1$

however, if $f^{-1}(x)=\dfrac{1}{2}\ln{x}$, then $ f^{-1}(e) = \dfrac{1}{2} \ne 1$

have another look ...

 

[karush]

https://www.physicsforums.com/attachments/9567

ok looks like your suggestion of $y=x^{2x}$ is correct

 

[HallsofIvy]

ok looks like your suggestion of $y=x^{2x}$ is correct

And that was not what he suggested! Please be more careful what you are writing or you are just wasting our time!

 

[karush]

post #2 looks like a suggestion to me!

 

[HallsofIvy]

Yes, but post 2 suggested that the original problem might be to find the inverse function of $$f(x)= e^{2x}$$, not of $$f(x)= x^{2x}$$ as you say in post 5!

 

[I like Serena]

Yes, but post 2 suggested that the original problem might be to find the inverse function of $$f(x)= e^{2x}$$, not of $$f(x)= x^{2x}$$ as you say in post 5!

I inspected the pdf. It looks to me that the typo is in the original problem.
That is, I think the writers of the pdf made the mistake.
We can only guess about what it should have been.

 

[HallsofIvy]

But i don't see anything in the first post that is connected with $$x^{2x}$$.

 

[I like Serena]

But i don't see anything in the first post that is connected with $$x^{2x}$$.

Ah yes. That's true. That was a typo when referring to a suggested possible typo about a typo in the opening post that was actually a presumed typo in the original pdf.