9.4.5 Identify the equilibrium values

[karush]

$\tiny{9.4.5}$
$$y'=\sqrt{5},y>0$$
Identify the equilibrium values
which are stable and unstable?

I assume 0 is the only one

 

[HallsofIvy]

Why would you "assume" that? Are you clear on what an equilibrium solution is?

An "equilibrium" position is one that does not change, such as a ball sitting at the top of a hill or at the bottom of valley as opposed to a ball on the side of the hill or the valley.
An equilibrium position is "stable" if a slight change from that equilibrium position does not result is a large change and "unstable" if it does. The ball sitting on the top of a hill is in an "unstable equilibrium" because as soon as it moves off the top it will roll all the way down the hill. A ball sitting at the bottom of a valley is in a "stable equilibrium" because if it moves slightly from that position, it will quickly roll back to the bottom.

An "equilibrium solution" to a differential equation is a constant solution- if y(t) is an equilibrium solution then y'= 0. Here we are told that y'= \sqrt{5}, a non-zero constant. Since y' is never 0 there is no equilibrium solution.

 

[karush]

that was helpful
l have more to do so hope it sinks in

the next one is$\tiny{9.4. 7}$
$$y'=(y-3)(y-4)(y-5)$$
identify the equilibrium values
3,4,5
which are stable and which are unstable?

 

[MarkFL]

Let's look at the behavior of the solutions near the equilibrium solution $y=3$. Suppose we have:

$$y(0)=2.9$$

Then we see:

$$y'<0$$

And for:

$$y(0)=3.1$$

We find:

$$0<y'$$

So, we find solutions are moving away from $y=3$, so that's an unstable equilibrium solution. What do you find near the other equilibrium solutions?

 

[HallsofIvy]

that was helpful
l have more to do so hope it sinks in

the next one is$\tiny{9.4. 7}$
$$y'=(y-3)(y-4)(y-5)$$
identify the equilibrium values
3,4,5
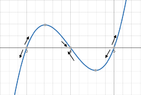
which are stable and which are unstable?

Okay, 3, 4, and 5 are equilibrium values because:
when y= 3, y'= (3- 3)(3- 4)(3- 5)= 0
when y= 4, y'= (4- 3)(4- 4)(4- 5)= 0
when y= 5, y'= (5- 3)(5- 4)(5- 5)= 0.

Now, if y< 3, all of y- 3, y- 4, and y- 5 are negative and the product of three negative numbers is negative. For y< 3, y'< 0.

If 3< y< 4, y- 3 is positive while y- 4 and y- 5 are still negative. The product of two negative and one positive number is positive. For 3< y< 4, y'> 0.

Think about what that means. If y is close to 3 but a little less than 3, y' is negative so y is decreasing, moving away from 3. If y is close to 3 but a little more than 3, y' is positive so y is increasing, moving away from 3. In either case, y is moving away from 3. y= 3 is an unstable equilibrium.

If 4< y< 5, both y- 3 and y- 4 are positive while y- 5 is still negative. The product of two positive and one negative number is negative. For 4< y< 5, y'< 0.

Now, if y is close to 4 but less than 4, y' is positive so y is increasing, moving toward 4. If y is close to 4 but a little more than 4, y' is negative so y is decreasing, moving toward 4. 4 is a stable equilibrium.

Finally, for y> 5, all three of y- 3, y- 4, and y- 5 are positive. The product of three positive numbers is positive. For y> 5, y'> 0.

So if y is close to 5 but less than 5, y'< 0 so y is decreasing, moving away from 5. If y' is close to 5 but more than 5, y'> 0 so y is increasing, moving away from 5. y= 5 is an unstable equilibrium.

 

[karush]

much mahalo
great help much more ready for test

which is tomorrow...yikes

 

[MarkFL]

much mahalo
great help much more ready for test

which is tomorrow...yikes

Here's the method I was taught as a student:

1.) Graph $$y'=f(y)$$.

2.) Near the roots, where $$f(y)<0$$ draw an arrow along the curve, in the direction of decreasing $y$ and where $$0<f(y)$$ draw an arrow along the curve in the direction of increasing $y$.

For this problem, we would have:

View attachment 6443

Now it's easy to see that:

• $$y=3$$ is unstable.
• $$y=4$$ is stable.
• $$y=5$$ is unstable.

 

[karush]

well that sure made it less confusing

looks like Desmos
how did you put in the arrows?

the colors looked the same to me??

 

[MarkFL]

well that sure made it less confusing

looks like Desmos
how did you put in the arrows?

the colors looked the same to me??

Yes, I used the Desmos calculator to generate the curve, then grabbed a screenshot and edited the image to add the arrows. If I had had more time, I would have tried to do it using TikZ. :D