- #1
Tunalover
- 11
- 1
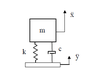
Consider a simple single degree-of-freedom (SDOF) spring-mass-dashpot dynamic system with spring rate k, mass m, and viscous damping coefficient c. Dimension x is the absolute displacement of the mass. The base input translation is y. A dot notation indicates differentiation with respect to time, t.
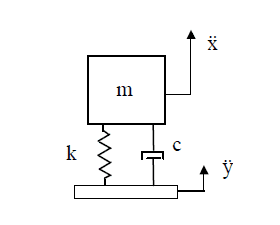
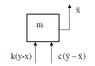
A free body diagram of the mass is:
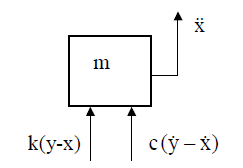
and the base input acceleration is a half-sine pulse of magnitude A and duration T:
$$ y=\begin{cases} Asin \frac {\pi t} T, ~0 \le \ t \le \ T \\
0,~ t \gt T \end{cases} $$
Determine the displacement x as a function of time t:
This system is actually a reasonably realistic simulation of the response of a suspension system from an impact of duration T.
The free body diagram summation of forces provides the following ODE:
$$ m \ddot x = k(y-x) + c(\dot y - \dot x) $$
To simplify the problem, make the following substitutions:
Let ## z=x-y, ## then ## \dot z=\dot x -\dot y ##, and ## \ddot z = \ddot x - \ddot y ##.
After making these substitutions and simplifying,
$$ m \ddot z + c \dot z + kz = -m \ddot y$$
To put this in more traditional form,
$$ \ddot z + \frac c m \dot z + \frac k m z=- \ddot y $$
The ratios of constants appear often in vibration theory and they are related to the natural frequency ## \omega_n ## (rad/sec), and dimensionless critical damping ratio ## \xi ## as follows:
$$ \omega^2_n = \frac k m $$ and
$$ \frac c m = 2 \xi \omega_n $$
then the ODE appears like this after substituting:
$$ \ddot z + 2 \xi \omega_n \dot z + \omega^2_n z = -2 \xi \omega_n \ddot y $$
and the final form is:
$$ \ddot z + 2 \xi \omega_n \dot z + \omega^2_n z = -2 \xi \omega_n
\begin{cases} Asin \frac {\pi t} T, ~0 \le \ t \le \ T \\
0,~ t \gt T \end{cases} $$
This is as far as I'm taking it. Take this the rest of the way on your own and let me know how it turns out for you. I'm not really looking for the solution but I'm rather putting this out there as a challenge to all mathematically-inclined forum participants. I'll put forward the solution in an attachment a few months from now or to anyone who contacts me asking for it before then. If you find a published solution please do not post to this thread and spoil it for everyone!
A free body diagram of the mass is:
and the base input acceleration is a half-sine pulse of magnitude A and duration T:
$$ y=\begin{cases} Asin \frac {\pi t} T, ~0 \le \ t \le \ T \\
0,~ t \gt T \end{cases} $$
Determine the displacement x as a function of time t:
This system is actually a reasonably realistic simulation of the response of a suspension system from an impact of duration T.
The free body diagram summation of forces provides the following ODE:
$$ m \ddot x = k(y-x) + c(\dot y - \dot x) $$
To simplify the problem, make the following substitutions:
Let ## z=x-y, ## then ## \dot z=\dot x -\dot y ##, and ## \ddot z = \ddot x - \ddot y ##.
After making these substitutions and simplifying,
$$ m \ddot z + c \dot z + kz = -m \ddot y$$
To put this in more traditional form,
$$ \ddot z + \frac c m \dot z + \frac k m z=- \ddot y $$
The ratios of constants appear often in vibration theory and they are related to the natural frequency ## \omega_n ## (rad/sec), and dimensionless critical damping ratio ## \xi ## as follows:
$$ \omega^2_n = \frac k m $$ and
$$ \frac c m = 2 \xi \omega_n $$
then the ODE appears like this after substituting:
$$ \ddot z + 2 \xi \omega_n \dot z + \omega^2_n z = -2 \xi \omega_n \ddot y $$
and the final form is:
$$ \ddot z + 2 \xi \omega_n \dot z + \omega^2_n z = -2 \xi \omega_n
\begin{cases} Asin \frac {\pi t} T, ~0 \le \ t \le \ T \\
0,~ t \gt T \end{cases} $$
This is as far as I'm taking it. Take this the rest of the way on your own and let me know how it turns out for you. I'm not really looking for the solution but I'm rather putting this out there as a challenge to all mathematically-inclined forum participants. I'll put forward the solution in an attachment a few months from now or to anyone who contacts me asking for it before then. If you find a published solution please do not post to this thread and spoil it for everyone!