Leo Liu
- 353
- 156
- Homework Statement
- .
- Relevant Equations
- .
Define that $$w(x,y,z)=zxe^y+xe^z+ye^z$$
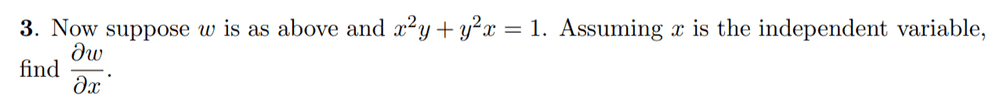
So the constraint equation is ##x^2y+y^2x=1##. And its differential is ##dy=-\frac{2xy+y^2}{2xy+x^2}##.
However, the solution plugs in ##z=0## when computing ##\frac{\partial w}{\partial x}## as shown in the screenshot below. While I understand that ##dz=0##, I can't see why ##z=0##. Could anyone explain?
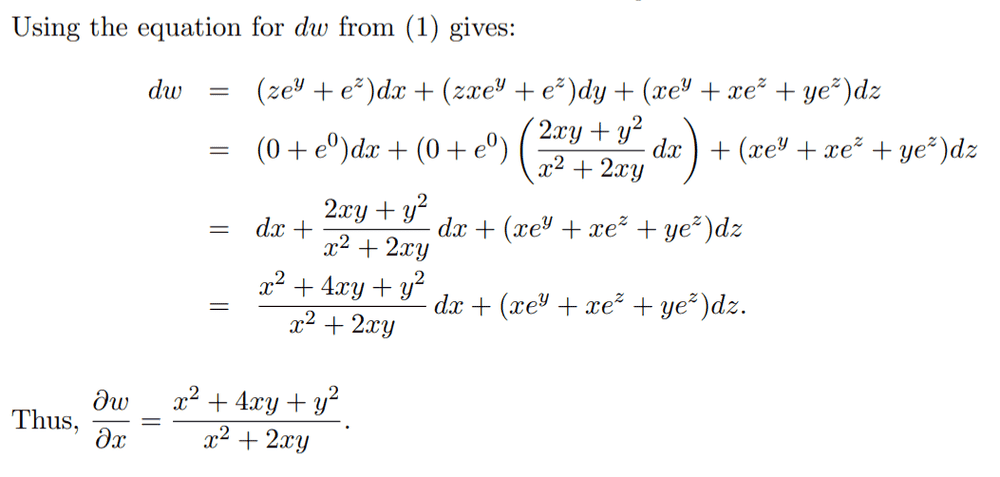
So the constraint equation is ##x^2y+y^2x=1##. And its differential is ##dy=-\frac{2xy+y^2}{2xy+x^2}##.
However, the solution plugs in ##z=0## when computing ##\frac{\partial w}{\partial x}## as shown in the screenshot below. While I understand that ##dz=0##, I can't see why ##z=0##. Could anyone explain?