A couple of questions about photons and superposition..

[Karagoz]

There are two polarization filters, A and B.

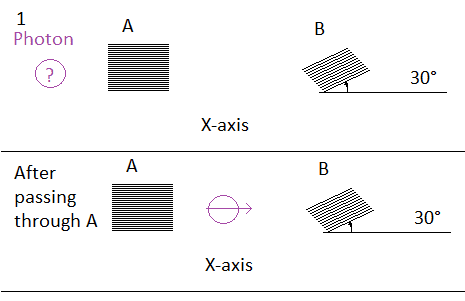
Polarization filter A has angle of 0° and B has an angle of 30°.

A photon is in superposition, so it doesn't have a definite polarization axis. The likelihood it's passing through a filter is depend on the difference between angle of the polarization filter A and angle of the polarization axis of photon.

But let's say the photon did pass through the filter A, and the photon's axis is now parallell with the filter A's axis (and X axis).

After passing through filter A, is that photon still in a superposition, or does this photon now have a definite polarization axis, or is it still in superposition?

The likelihood P of that photon passing through polarization filter B, is it P = cos^2(30°) = 0.75 ?

 

[Nugatory]

After passing through filter A, is that photon still in a superposition, or does this photon now have a definite polarization axis, or is it still in superposition?

After it passes through the first filter, it is in the state "100% chance of passing through a horizontally oriented filter". That state is not a superposition of horizontally polarized and vertically polarized. However, it is a superposition of polarization along other axes. In particular, it is equal to $\frac{\sqrt{3}}{2}|30\rangle+\frac{1}{2}|120\rangle$ where $|30\rangle$ is the state "100% chance of passing through a filter at 30 degrees from horizontal" and $|120\rangle$ is the state "100% chance of passing through a filter perpendicular to 30 degrees". Apply the Born rule to that superposition and you will see that the photon does in fact have a .75 probability of passing the 30-degree filter.

(Note that I have carefully avoided saying that the photon has a definite polarization in any direction. It never does - "100% chance of passing through a horizontally oriented filter" is not the same thing as "definitely polarized on a horizontal axis")

 

[Derek P]

(Note that I have carefully avoided saying that the photon has a definite polarization in any direction. It never does - "100% chance of passing through a horizontally oriented filter" is not the same thing as "definitely polarized on a horizontal axis")

Unless that's what you define "definite polarisation" as... Just sayin'.

 

[Khashishi]

Whether something is in superposition depends on your choice of basis states. A state could be in superposition in one set of basis states and not in another.

 

[Nugatory]

Unless that's what you define "definite polarisation" as... Just sayin'.

Fair enough, but do you want to take a B-level thread into that swamp? :)
The mathematical formalism says what I said and no more, so that's as much as I'm going to say in this thread.

 

[DrChinese]

Fair enough, but do you want to take a B-level thread into that swamp? :)

Nooooo... We need to drain that swamp.

PS As I go to "like" your post, I realize you are at 3500 likes already. Impressive.

 

[kent davidge]

3500 likes

3,502 actually