- #1
Karagoz
- 52
- 5
It’s written almost all physics books and courses that entangled photons can’t be used for faster than light communication. The question about used entangled photons to communicate faster than light has been discussed before, but I didn’t get exactly why faster than light communication with entangled photons is impossible.
My goal is not to prove so many physicists and scientists that they’re wrong about entangled photons can’t be used to faster than light communication, nor to show that I have “invented” a way to entangled photons for faster than light communication.
From my superficial knowledge on quantum physics:
The probability P for a photon to pass through the filter depends on the angle Φ between the photon and the filter polarization axis:P = cos^2(Φ)
Imagine some photons that are entangled and sent far away with Jack and Joe.
They have agreed beforehand that they’ll send message to each other every 24 hours (or every 12 pm)
Jack has some photons, and Joe has other photons. The photons are entangled:
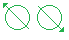
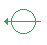
Jack will give a signal to Joe, 0 or 1.
The signal is 0 when he passes his photon through a filter like this, and changes its axis:

The likelihood of the photon passing through is %50, because Φ = 45 degrees.
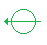
If Jack’s photon passes through the filter and changes its axis, then Joe’s photon will change to this axis:

The signal is 1 is when he passes his photon through a filter like this, and changes its axis:

The likelihood of the photon passing through is %50, because Φ = 45 degrees.
If Jack’s photon passes through the filter and changes its axis, then Joe’s photon will change to this axis:
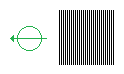
After 12 pm Jack sends his photon through a filter. It’s going to pass through it by chance of %50 (since Φ = 45 degrees). He use polarizing beam splitter to test same photon again and again until it passes through the filter. So if the photon doesn’t pass in the first time, Jack tries the same photon again and again until it passes through it.When Jack’s photons pass through the filter, the axis of the photon changes. When axis of Jack’s photon changes, so does Joe’s photon change its axis too.
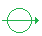
After 12 pm Joe knows that his photon has changed its axis because Jack sent him a message. But Joe doesn’t know the axis of his photon.Joe passes his photon through a filter like this:

If his photon is changed to this axis:

Then it’s %100 likely his photon will pass through that filter.
If his photon is changed to this axis:
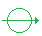
Then it’s %100 likely his photon won’t pass through the filter.So by trying to get the phtoton pass the filter, Joe will know what message is sent from Jack (whether it’s 0 or 1).Now Jack’s photons is one of this axis:
 or
or
He can pass his photon through another filter and change reset the photons axis again. He can use polarizing beam splitter to try same photon again and again until it passes through the filter and changes its axis:

Jack can repeat this process again next day, and send a message (0 or 1) next day.
By increasing the number of photons, Jack can increase the number of 0s and 1s, and he can send codes that can be interpreted as full messages.
Or is there something I’m missing or taking it wrong?
My goal is not to prove so many physicists and scientists that they’re wrong about entangled photons can’t be used to faster than light communication, nor to show that I have “invented” a way to entangled photons for faster than light communication.
From my superficial knowledge on quantum physics:
The probability P for a photon to pass through the filter depends on the angle Φ between the photon and the filter polarization axis:P = cos^2(Φ)
Imagine some photons that are entangled and sent far away with Jack and Joe.
They have agreed beforehand that they’ll send message to each other every 24 hours (or every 12 pm)
Jack has some photons, and Joe has other photons. The photons are entangled:
Jack will give a signal to Joe, 0 or 1.
The signal is 0 when he passes his photon through a filter like this, and changes its axis:
The likelihood of the photon passing through is %50, because Φ = 45 degrees.
If Jack’s photon passes through the filter and changes its axis, then Joe’s photon will change to this axis:
The signal is 1 is when he passes his photon through a filter like this, and changes its axis:
The likelihood of the photon passing through is %50, because Φ = 45 degrees.
If Jack’s photon passes through the filter and changes its axis, then Joe’s photon will change to this axis:
After 12 pm Jack sends his photon through a filter. It’s going to pass through it by chance of %50 (since Φ = 45 degrees). He use polarizing beam splitter to test same photon again and again until it passes through the filter. So if the photon doesn’t pass in the first time, Jack tries the same photon again and again until it passes through it.When Jack’s photons pass through the filter, the axis of the photon changes. When axis of Jack’s photon changes, so does Joe’s photon change its axis too.
After 12 pm Joe knows that his photon has changed its axis because Jack sent him a message. But Joe doesn’t know the axis of his photon.Joe passes his photon through a filter like this:
If his photon is changed to this axis:
Then it’s %100 likely his photon will pass through that filter.
If his photon is changed to this axis:
Then it’s %100 likely his photon won’t pass through the filter.So by trying to get the phtoton pass the filter, Joe will know what message is sent from Jack (whether it’s 0 or 1).Now Jack’s photons is one of this axis:
He can pass his photon through another filter and change reset the photons axis again. He can use polarizing beam splitter to try same photon again and again until it passes through the filter and changes its axis:
Jack can repeat this process again next day, and send a message (0 or 1) next day.
By increasing the number of photons, Jack can increase the number of 0s and 1s, and he can send codes that can be interpreted as full messages.
Or is there something I’m missing or taking it wrong?
Attachments
-
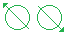 upload_2018-4-10_20-16-1.png227 bytes · Views: 634
upload_2018-4-10_20-16-1.png227 bytes · Views: 634 -
 upload_2018-4-10_20-16-17.png314 bytes · Views: 635
upload_2018-4-10_20-16-17.png314 bytes · Views: 635 -
 upload_2018-4-10_20-16-36.png156 bytes · Views: 1,118
upload_2018-4-10_20-16-36.png156 bytes · Views: 1,118 -
 upload_2018-4-10_20-17-59.png327 bytes · Views: 655
upload_2018-4-10_20-17-59.png327 bytes · Views: 655 -
 upload_2018-4-10_20-19-3.png157 bytes · Views: 1,124
upload_2018-4-10_20-19-3.png157 bytes · Views: 1,124 -
 upload_2018-4-10_20-19-29.png256 bytes · Views: 626
upload_2018-4-10_20-19-29.png256 bytes · Views: 626 -
 upload_2018-4-10_20-19-38.png189 bytes · Views: 640
upload_2018-4-10_20-19-38.png189 bytes · Views: 640 -
 upload_2018-4-10_20-19-51.png191 bytes · Views: 638
upload_2018-4-10_20-19-51.png191 bytes · Views: 638 -
 upload_2018-4-10_20-20-25.png159 bytes · Views: 627
upload_2018-4-10_20-20-25.png159 bytes · Views: 627 -
 upload_2018-4-10_20-20-34.png163 bytes · Views: 629
upload_2018-4-10_20-20-34.png163 bytes · Views: 629 -
 upload_2018-4-10_20-20-44.png332 bytes · Views: 612
upload_2018-4-10_20-20-44.png332 bytes · Views: 612