- #1
Karagoz
- 52
- 5
In quantum physics they say that the probability P for a photon to pass through the filter depends on the angle Φ between the photon and the filter polarization axis:
P = cos^2(Φ)
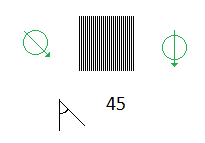
And if I'm not wrong, when the photon passes through that filter (like illustrated in the image above) the photon will change its polarization axis.
In the picture above where the Φ = 45°, then P = 0.5
So if we let one single photon try passing through that filter, then the probability of it passing through the filter is 50% (P = 0.5)
So if we have 1000 photons, then we can say that ca 50% will pass through that filter since the probability is 50%.
But those photons that didn't pass through the filter, if we try them passing the same filter, will they pass through the filter?
I mean let's say that one single photon (where Φ = 45°) didn't pass through the filter (since there's 0.5 chance it doesn't). If we try with the same photon again and again the photon will never pass through that filter since it didn't pass through it first time?
P = cos^2(Φ)
And if I'm not wrong, when the photon passes through that filter (like illustrated in the image above) the photon will change its polarization axis.
In the picture above where the Φ = 45°, then P = 0.5
So if we let one single photon try passing through that filter, then the probability of it passing through the filter is 50% (P = 0.5)
So if we have 1000 photons, then we can say that ca 50% will pass through that filter since the probability is 50%.
But those photons that didn't pass through the filter, if we try them passing the same filter, will they pass through the filter?
I mean let's say that one single photon (where Φ = 45°) didn't pass through the filter (since there's 0.5 chance it doesn't). If we try with the same photon again and again the photon will never pass through that filter since it didn't pass through it first time?
