A Fact I Observed While Looking at the Proof of the Pythagorean Theorem.

[caffeinemachine]

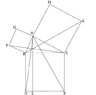
Let $ABC$ be a right angled triangle, where the right angle is at $A$.
Construct squares on $AC$, $AB$ and $BC$ as shown. Let $P$ be the point of intersection of $BK$ and $FC$ (Note that $P$ is not marked in the figure).

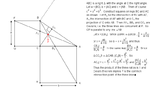
Then I conjecture that $AP$ is parallel to $BD$.View attachment 4630What I tried:By obsercing that $\Delta FBC\cong \Delta ABD$, we see that $\angle BAC=\angle BFC$.
Therefore, if $X$ is the point of intersection of $FC$ and $AD$, we see that $BFAX$ is a cyclic quadrilateral.This gives us that $AD\perp FC$, and similarly $BK\perp AE$. But I couldn't go any further.

 

[Opalg]

Your conjecture is correct (but this is not the sort of proof that you wanted).

I took coordinates with $B$ as the origin, and $C = (1,0)$. If $\theta$ is the angle $ABC$ then $A = (\cos^2\theta, \sin\theta\cos\theta)$, $F = (-\sin\theta\cos\theta, \cos^2\theta)$ and $K = (1+\sin\theta\cos\theta, \sin^2\theta).$ The equation of the line $CF$ is $y(1+\sin\theta\cos\theta) = (1-x)\cos^2\theta$, and the equation of $BK$ is $y(1+\sin\theta\cos\theta) = x\sin^2\theta.$ The $x$-coordinate of the point $P$ where these lines intersect is $\cos^2\theta$, which is the same as the $x$-coordinate of $A$. This shows that $AP$ is perpendicular to $BC$ and therefore parallel to $BD$.

I don't know if there is anything about that proof that might help in finding a Euclidean proof of the result. The proof must somehow exploit the fact that there is a right angle at $A$, and I don't see how to bring that in.

 

[caffeinemachine]

Your conjecture is correct (but this is not the sort of proof that you wanted).

I took coordinates with $B$ as the origin, and $C = (1,0)$. If $\theta$ is the angle $ABC$ then $A = (\cos^2\theta, \sin\theta\cos\theta)$, $F = (-\sin\theta\cos\theta, \cos^2\theta)$ and $K = (1+\sin\theta\cos\theta, \sin^2\theta).$ The equation of the line $CF$ is $y(1+\sin\theta\cos\theta) = (1-x)\cos^2\theta$, and the equation of $BK$ is $y(1+\sin\theta\cos\theta) = x\sin^2\theta.$ The $x$-coordinate of the point $P$ where these lines intersect is $\cos^2\theta$, which is the same as the $x$-coordinate of $A$. This shows that $AP$ is perpendicular to $BC$ and therefore parallel to $BD$.

I don't know if there is anything about that proof that might help in finding a Euclidean proof of the result. The proof must somehow exploit the fact that there is a right angle at $A$, and I don't see how to bring that in.

Hey Opalg. Take a look at this. geometry - A Fact I Observed While Looking at the Proof of Pythagorean Theorem. - Mathematics Stack Exchange

 

[Opalg]

Hey Opalg. Take a look at this. geometry - A Fact I Observed While Looking at the Proof of Pythagorean Theorem. - Mathematics Stack Exchange

Very neat! When I see a really clever proof like that, it reminds me of how much Euclidean geometry appealed to me in high school sixty years ago. In Britain, this sort of geometry does not feature in school mathematics at all any more. I think that is a great pity, because it is such a good way to attract (some) students to mathematics and to teach them the concept of proof.

 

[caffeinemachine]

Very neat! When I see a really clever proof like that, it reminds me of how much Euclidean geometry appealed to me in high school sixty years ago. In Britain, this sort of geometry does not feature in school mathematics at all any more. I think that is a great pity, because it is such a good way to attract (some) students to mathematics and to teach them the concept of proof.

I share the sentiment Opalg. In the wake of modern mathematics, Euclidean geometry is now not important in terms of research. Thus even some of the people good at math tend to ignore the subject.

 

[johng1]

CaffeineMachine, when I read your question it almost immediately occurred to me that Ceva's theorem,
Ceva's Theorem might be applicable. The following attachment shows that indeed this theorem implies the result. My apologies for changing notation, but for me a right triangle should satisfy $a^2+b^2=c^2$.

Classical geometry is a beautiful subject, and I really enjoy it. However, many people, even those like me with a mathematical bent, find the subject to be quite challenging. For beginning students even "simple" ideas like similar triangles can be confusing. It's bad enough to identify corresponding sides, but after that there are just too many equations involving the sides. So I think maybe it's a good idea to bypass geometry as a first course. I'm afraid too many beginning students in geometry say: if this is math, it's too hard for me.

View attachment 4642

 

[caffeinemachine]

CaffeineMachine, when I read your question it almost immediately occurred to me that Ceva's theorem,
Ceva's Theorem might be applicable. The following attachment shows that indeed this theorem implies the result. My apologies for changing notation, but for me a right triangle should satisfy $a^2+b^2=c^2$.

Classical geometry is a beautiful subject, and I really enjoy it. However, many people, even those like me with a mathematical bent, find the subject to be quite challenging. For beginning students even "simple" ideas like similar triangles can be confusing. It's bad enough to identify corresponding sides, but after that there are just too many equations involving the sides. So I think maybe it's a good idea to bypass geometry as a first course. I'm afraid too many beginning students in geometry say: if this is math, it's too hard for me.

That's just super nice and a bit more easy to come up with than the one I had given a link to.