A geometric proof (minimizing the length of two lines in a rectangle)

[ali PMPAINT]

Homework Statement

Show that in a rectrangular ABCD, with a point P on CD, Show that AP+BP is smallest when CP=DP

Relevant Equations

Maybe sin(a+b)=sin(a)cos(b)+cos(a)sin(b) and sin(a-b)=sin(a)cos(b)-cos(a)sin(b)

So, I know it can be proven using calculus, but I need the geometric one.

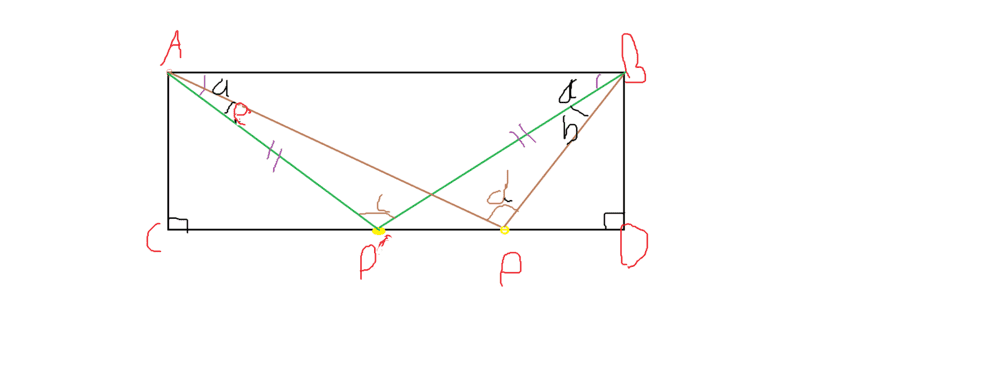
So, I got that ^c=^d and therefor, the amount of increment in one of a, is equal to the other(^e=^b). (Also 0<a+b<Pi/2)
And AP'=BP'=BD/sin(a) and BP=BD/sin(a+b) and AP=BD/sin(a-b).
AP'+BP'=2AP'=2BD/sin(a) and AP+BP=BD(1/sin(a+b)+1/sin(a-b))
Know I'm trying to show 1/sin(a+b)+1/sin(a-b)>2/sin(a) for 0<a+b<Pi/2 , But no result.
Any suggestion please?

 

[BvU]

Flip over the line CD to get A' and B' as corners of rectangle A'B'B A
What's the shortest line from A'to B ?

 

[ali PMPAINT]

Flip over the line CD to get A' and B' as corners of rectangle A'B'B A
What's the shortest line from A'to B ?

Thanks for the hint!

On triangle BP'A', we have BP'+A'P'>BA' and beacuase BA'=2BO=AO+BO , and BP'+A'P'=BP'+AP' , we get BP'+AP'>AO+BO