A Question about Albert Shadowitz's Explanation of Ampere's Law

[bryanso]

In Shadowitz's book The Electromagetic Field, Section 3-4, p. 129 to 134, there is a very interesting derivation of Ampere's Law. It is a general derivation with a circular source circuit S, and a circular test circuit T. The pages can be seen here, at least from where I post (USA):

https://books.google.com/books?id=k7XCAgAAQBAJ&pg=PA129&lpg=PA129#v=onepage&q&f=false

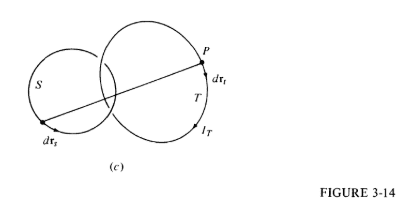
Briefly, starting from Biot-Savart Law, the circulation Integrate(B . dr_t) is calculated. At one point (dr_s x R_st . dr_t) / R² is replaced with the equivalent (dr_t x dr_s . R_st) / R². This the author turns first into (dS . R_ts) / R² then finally he equates this with dOmega the solid angle (bottom of p. 131). I am in agreement with this algebra.

(R_st and R_ts represent unit vectors)

Then comes a really interesting change of point-of-view. He explains if we hold P fixed (P is a point on the test circuit T) instead of moving P around T, then effectively it is the entire circuit S moving in space. And the complete movement is a torus. Figure 3-16.

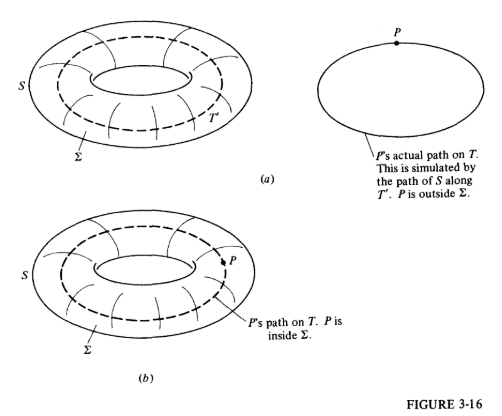
If S and T are linked (kind of like the magician's linking rings :) then the point P lies within the "torus".

He then equates Integrate(dOmega) to 4pi.

Now I am not able to convince myself or prove a solid angle inside a torus sum to 4pi. All online help I can find are integration of solid angles inside a sphere or a potato :) A torus is not the same because a cone from P will eventually go out of the torus and comes back into the opposite arm of the torus.

It's funny the author writes "This is also left for the student to prove..."

Thanks

 

[vanhees71]

I think this is overly and unnecessarily complicated. First of all fundamental laws cannot be "derived". They are condensed empirical wisdom. The most comprehensive wisdom about electromagnetism as far as classical physics is concerned are Maxwell's equations, of which the Ampere-Farday Law is a fundamental equation.

Maxwell's theory can a posteriory "derived" also from the information that it's an (on the fundamental level un-Higgsed) gauge theory with gauge group U(1).

Here, obviously the author uses a more historical approach (which is usually only interesting, if you are already familiar with the theory and want to learn about the history itself rather than the other way thinking it would help to understand the physics going through all the thorny paths our predecessors had to go to find out about it), i.e., he takes the Biot-Savart Law as the known law. It's of course only valid for the special case of magnetostatics (this as a warning).

Then I wouldn't formulate it with the singular form of a current through an infinitely thin wire, but just a continuous current density. Then in more comprehensible notation it reads (in Heaviside Lorentz units)
$$\vec{B}=\frac{1}{4 \pi c} \int_{\mathbb{R}^3} \mathrm{d}^3 r' \vec{j}(\vec{r}') \times \vec{\nabla} \frac{1}{|\vec{r}-\vec{r}'|}=-\frac{1}{4 \pi c} \vec{\nabla} \times \int_{\mathbb{R}^3} \mathrm{d}^3 r' \frac{\vec{j}(\vec{r}')}{|\vec{r}-\vec{r}'|}.$$
From this you get immediately Gauss's Law for the magnetic field (which is valid generally, not only in the here discussed static case)
$$\vec{\nabla} \cdot \vec{B}=0.$$
Knowing that the "source" vanishes, you now are also inclined to know the curl (at least if you familiar with Helmholtz's fundamental theorem of vector calculus). This brings you to the idea to calculate the curl:
$$\vec{\nabla} \times \vec{B} =-\frac{1}{4 \pi c} \int_{\mathbb{R}^3}
\mathrm{d}^3 r' \left [ \vec{\nabla} \left (\vec{j}(\vec{r}') \cdot \vec{\nabla}
\frac{1}{|\vec{r}-\vec{r}'|} \right) -\vec{j}(\vec{r}')
\Delta \frac{1}{|\vec{r}-\vec{r}'|} \right]. $$
The second term is well-known from electrostatics. From the Coulomb Law of a point charge you know that
$$\Delta \frac{1}{|\vec{r}-\vec{r}'|}=-4 \pi \delta^{(3)}(\vec{r}-\vec{r}').$$
For the first term we note that
$$
\int_{\mathbb{R}^3}
\mathrm{d}^3 r' \vec{\nabla} \left (\vec{j}(\vec{r}') \cdot \vec{\nabla}
\frac{1}{|\vec{r}-\vec{r}'|} \right) = -\vec{\nabla} \int_{\mathbb{R}^3} \vec{j}(\vec{r}') \cdot \vec{\nabla}' \frac{1}{|\vec{r}-\vec{r}'|}=+\vec{\nabla} \int _{\mathbb{R}^3} \mathrm{d}^3 r' \frac{1}{|\vec{r}-\vec{r}'|}\vec{\nabla}' \cdot \vec{j}(\vec{r}')=0,$$
where we have integrated by parts and then used $\vec{\nabla} \cdot \vec{j}=0$, which holds due to charge conservation for the static case (i.e., for $\partial_t \rho=0$).

After this cumbersome analysis finally you find Ampere's Law
$$\vec{\nabla} \times \vec{B}=\frac{1}{c} \vec{j}.$$

 

[bryanso]

Thanks. Any recommended textbook that teaches this topic in a more modern viewpoint, as a prerequisite before tackling more advanced topics?

 

[vanhees71]

I think on the undergrad level Griffiths's book is very good. Also the Feynman lectures. On the graduate level I'd recommend Landau&Lifshitz vol. 2 (for the macroscopic theory vol. 8). Then there's of course also Jackson, which is the standard reference though to my taste bringing relativity too late.

 

[bryanso]

Thanks a lot!