- #1
DirecSa
- 12
- 2
I'm reading about the derivation of ampere force law formula, which is $$ F=k_A \iint \frac{i'ds' \times (ids \times \vec{r})}{\vec{r}^2}$$ where K_A is mu_0/4pi. In the article that I read, they have assumed such these paths:
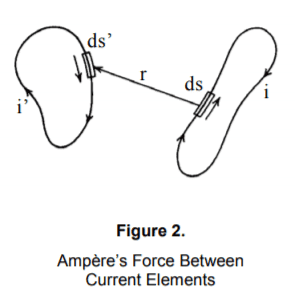
And according to ampere's conclusion that he had from observation is that the effect of a current flowing in a circuit twisted into small sinuosities is the same as if the circuit were smoothed out. And then in the article they came up with the following equation (A1):

So I guess that it came from vectors analysis, but I can't actually figure out how they got it...! In addition, my second question would be about equations (A3), why it would be the guess and why they are the simplest forms and not for example 1/r^2?
I would be grateful for explanations and thank you in advance.
The article is: Derivation of the Universal Force Law—Part 2 Charles W. Lucas, Jr. 29045 Livingston Drive Mechanicsville, MD 20659-3271
And according to ampere's conclusion that he had from observation is that the effect of a current flowing in a circuit twisted into small sinuosities is the same as if the circuit were smoothed out. And then in the article they came up with the following equation (A1):
So I guess that it came from vectors analysis, but I can't actually figure out how they got it...! In addition, my second question would be about equations (A3), why it would be the guess and why they are the simplest forms and not for example 1/r^2?
I would be grateful for explanations and thank you in advance.
The article is: Derivation of the Universal Force Law—Part 2 Charles W. Lucas, Jr. 29045 Livingston Drive Mechanicsville, MD 20659-3271
Last edited: