- 2,163
- 191
Homework Statement
The Zacchini family was renowned for their human-cannonball act in which a family member was shot from a cannon using either elastic bands or compressed air.In one version of the act,Emanuel Zacchini was shot over three Ferris wheels to land in a net at same height as the open end of the cannon and at a range of 69 m.He was propelled inside the barrel for 5.2 m and launched at an angle of 530 ( degree).If his mass was 85 kg and he underwent cosntant acceleration inside the barrel,what was the magnitude of the force propelling him ? ( Hint:Treat the launch as though it were along aa ramp at 530 ( degree).Neglect air drag )
Homework Equations
\vec F_t=m \vec a m=mass \vec F_t =Total \ Force
\vec w_=m \vec g g=9.8 m/s^2
v-v_0=at v_0=inital \ velocity
Projectile motion equations (In this question they will be in different forms I guess and I don't know how to find them that's my problem)
The Attempt at a Solution
[/B]
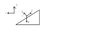
I upload a picture.After that solution I am stucked.Cause there's acceleration and also velocity of the object and I have to apply them to projectile motion equations.
Here my try
For x-axis ;
69m=v_0cos(53^0) t+\frac 1 2 acos(53^0)t^2
Simply I couldn't solve.
For y axis;
Here things are more complicated
Simply I couldn't solve.
Also another referance frame would be easier to solve but I couldn't put the forces in there something's doesn't make sense.I would be happy If somebody help me
Thanks