A triangle problem: Prove that |AC|+|AB|=|PR|+|PQ| given some constraints

[wrobel]

I actually do not understand where to place this thread. Hope that it is a high school level problem.

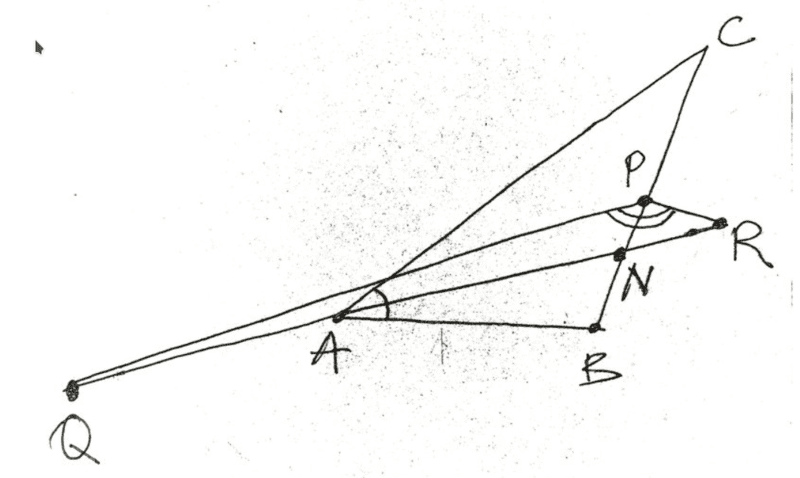
There are two triangles ABC and PQR. The vertex A is a middle of the side QR. The vertex P is a middle of the side BC. The line QR is a bisector of the angle BAC. The line BC is a bisector of the angle QPR. Prove that |AC|+|AB|=|PR|+|PQ|.

Using vector algebra methods and huge symbolic calculations in Maple I proved this fact in an additional assumption:
there are no parallel lines among AC, AB, PR, PQ.

I am sure that my method is not adequate and there must be an elementary high-school-level solution but I do not see it.

Please comment.

 

[Steve4Physics]

There are two triangles ABC and PQR. The vertex A is a middle of the side QR. The vertex P is a middle of the side BC. The line QR is a bisector of the angle BAC. The line BC is a bisector of the angle QPR. Prove that |AC|+|AB|=|PR|+|PQ|.

The first step could be to produce a diagram. Can you do that and post it here?

Apologies - didn't see diagram till just now.

 

[Lnewqban]

....there must be an elementary high-school-level solution but I do not see it.
Please comment.

Could this be an easier way?:
https://en.m.wikipedia.org/wiki/Angle_bisector_theorem

I have reached the following point:

QA = AR

BP = PC

CN / BN = AC / AB

RN / QN = PR / PQ

 

[Throwaway_for_June]

Assuming that CB is not parallel to QR, there has to be a circle that goes through all four points of those points. Maybe drawing in that circle leads somewhere.

 

[Throwaway_for_June]

Looking at this a little more, there should also be a single circle centered on N that's tangent to QP, PR, AB, and AC.

Can you construct an example of this geometry where ABC and PQR are different?

 

[Throwaway_for_June]

We know that there's an "outer circle" that goes through QBRC, and we know that there's an "inner circle" that is tangent to AB, AC, PQ, and PR. The "inner circle" is centered at N, and the outer circle is centered

WOLOG, we can assume that the radius of the outer circle is 1. And, let's say that we start by picking some lengths BN and NP that we want to generate a diagram for.

Then we have $\overline{\rm{OP}} = \sqrt{1-\overline{\rm{BP}}^2}$.

And, I don't have clean formula for it to hand, but that leaves only one possible angle for PQR that makes the segment QR go through N. That, in turn, fixes the location of A, but we don't have any guarantee that QR bisects BAC yet. Ensuring that it is will probably "use up" one more degree of freedom.

 

[wrobel]

Assuming that CB is not parallel to QR, there has to be a circle that goes through all four points of those points. Maybe drawing in that circle leads somewhere.

why?

Then we have OP―=1−BP―2.

a vector is equal to a number hm

my bad solution: UPDATED the critical case with parallel lines is added

 

[Throwaway_for_June]

why?

Ugh. I guess I'm too used to thinking about triangles where there are shared vertices. So there's no shared inner or outer circle, but concentric pairs of circles instead.

 

[Throwaway_for_June]

So, if $\delta=\angle QPN$, $\gamma = \angle CAN$ and $\alpha=\angle ANP$ then I think we have

$\left| \bar{QP }\right| + \left|\bar{PR}\right| =2 \frac{\sin \alpha}{\sin \delta} \left| \bar{AN} \right| + 2 \frac{sin \alpha}{\sin \left(\alpha - \delta \right)} \left| \bar{NP} \right|$
and
$\left| \bar{AB }\right| + \left|\bar{AC}\right| =2 \frac{\sin \alpha}{\sin \gamma} \left| \bar{NP} \right| + 2 \frac{sin \alpha}{\sin \left(\alpha - \gamma \right)} \left| \bar{AN} \right|$

from the law of sines and some algebra.

Those are symmetric, so $\alpha = \delta + \gamma$ would give the desired result, but, unfortunately, that doesn't seem to hold in general.

If I try to construct the two triangles starting with some $A$, $N$ and $P$ I end up with a big quadratic that doesn't simplify in any ways that are obvious to me, so I'm not sure that there is any answer that's cleaner than what maple came up with.

 

[hutchphd]

I do so want to use Ptolemy's Theorem on this but unfortunately I can't even get close.

 

[Throwaway_for_June]

I do so want to use Ptolemy's Theorem on this but unfortunately I can't even get close.

I was looking for cross ratio stuff, but I don't think that's there either.

 

[Throwaway_for_June]

I do so want to use Ptolemy's Theorem on this but unfortunately I can't even get close.

I didn't realize that CQBR really are all on the same circle. Ptolemy's should work for showing that, but ...

For Ptolemy's theorem we want $\left| QC \right| \left| BR \right| + \left| QB \right| \left| RC \right| = \left| QR \right| \left| CB \right|$.

I imagine it's possible to use the law of cosines to find expressions for the outer edges of the quadrilateral, rewrite all the lengths in terms of $\left| AN \right|, \left| NR \right|, \left| PN \right| ,$ and $\left| NR \right|$ but that's going to work out to doing algebra with something like 64 terms which is doable in princple, but seems less than ideal.

It also doesn't readily get to the originally desired identity.

 

[Throwaway_for_June]

This smacks of "coffin problem."

Let's say that we start with $\bigtriangleup ABC$. Then it's easy to find the the perpendicular bisector of $BC$, the bisector of $\angle CAB$ , the perpendicular to that bisector $OA$ and then the circle centered at $O$ that goes through $B$ (or $C$).

Now we can extend $QP$ and $RP$ through the point $P$ to make points $R'$ and $Q'$ respectively. $PQR$ and $PQ'R'$ are obviously congruent (though I don't 100% have the justifcation for that). That will then give that $CB$ bisects $\angle QPR$ thanks to all of the vertical angles at $P$. $\bigtriangleup QPR$ is determined by $\bigtriangleup ABC$, so our construction of an example with $QBRC$ all on a circle shows that $QBRC$ is all on a circle.

Then we can imagine extending $QP$ past $P$ to make a chord of the circle with length $\left| QP \right| + \left| PR \right|$. There's an analogous chord for $\left| CA \right| + \left| AB \right|$.... Maybe there's a way to show that $AC$ and $QP$ are both the same distance from $O$.

Thanks for sharing the question. It's interesting.

 

[Throwaway_for_June]

OK, this is still a little ugly, but at least it all makes sense. $O$ - the place where the perpendicular bisectors meet - is also a the place where the circumcircles meet and there's also a connection between the angle bisectors, and the perpendicular bisectors as marked by the points $T$ and $E$.

With this diagram in hand it's not so hard to work out that $\left| OR \right|^2 = \left| OB \right|^2 = - \frac{ \left| OA \right| \left| OP \right| } { \cos{ \angle ANP } }$, so $QBRC$ are all on a circle centered at $O$.

The expression is symmetric with respect to $\left| OA \right|$ and $\left| OP \right|$, so it's sufficient to show that it works for one side.

$\left| OT \right| = - \frac { \left| OP \right| } {\cos{ \angle ANP } }$ from basic trig. Then since $OT$ is a diameter we can use Pythagoras' theorem:

$\left| OR \right|^2 = \left( \frac{ \left| OT \right| } {2} \right)^2 - \left( \frac{ \left| OT \right| } {2} - \left| OA \right| \right)^2 + \left| OA \right|^2 = 2 \frac{ \left| OT \right| } {2} \left| OA \right| = - \frac{ \left| OA \right| \left| OP \right| } { \cos{ \angle ANP } }$