hidemi
- 206
- 36
- Homework Statement
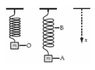
- A weight of mass m is at rest at O when suspended from a spring, as shown. When it is pulled down and released, it oscillates between positions A and B. Which statement about the system consisting of the spring and the mass is correct?
a. The gravitational potential energy of the system is greatest at A.
b. The elastic potential energy of the system is greatest at O.
c. The rate of change of momentum has its greatest magnitude at A and B.
d. The rate of change of gravitational potential energy is smallest at O.
e. The rate of change of gravitational potential energy has its greatest magnitude at A and B.
Ans: C
- Relevant Equations
- Eq.1 : U = -1/2 * kx^2
Eq.2 : dU/dt = -kx
I just would like to check if my corrections to each of the wrong options are right.
A) & B) elastic potential energy greatest at B, not at A or O, based upon Eq.1
D) Since dU/dt = 0 at O because O is at equilibrium where no change of spring length.
E) At A, dU/dt = -kx. At B, dU/dt = -kx = -kx
Therefore, I think the rate of change of gravitational potential energy is smallest at A and B greatest at O.
I'm not sure if these reasonings are ok?
A) & B) elastic potential energy greatest at B, not at A or O, based upon Eq.1
D) Since dU/dt = 0 at O because O is at equilibrium where no change of spring length.
E) At A, dU/dt = -kx. At B, dU/dt = -kx = -kx
Therefore, I think the rate of change of gravitational potential energy is smallest at A and B greatest at O.
I'm not sure if these reasonings are ok?