To find the distance of a horizontally suspended rod from a ceiling

[gnits]

Homework Statement

To find the distance of a horizontally suspended rod from a ceiling

Relevant Equations

Moments and equating of forces

Please could I ask for help with the following?

Two points, A and B on a horizontal ceiling are at a distance of 2a apart. A uniform rod CD of length a and weight W is suspended from A and B by two light strings AC, BD. A particle of weight (2/5)W is attached to the rod at D, and the system hangs in equilibrium with the rod horizontal. Prove that the rod is at a distance (6/7)a below the ceiling and find the inclination of BD. If both strings are elastic and of natural length (1/2)a, find the modulus of elasticity of each string in terms of W.

I have correctly found the inclination of BD (agree with answer in back of book) and if I assume the answer of (6/7)a then I can find the elastic moduli.

I cannot see how to prove that the distance from the ceiling is (6/7)a. Here's a diagram:

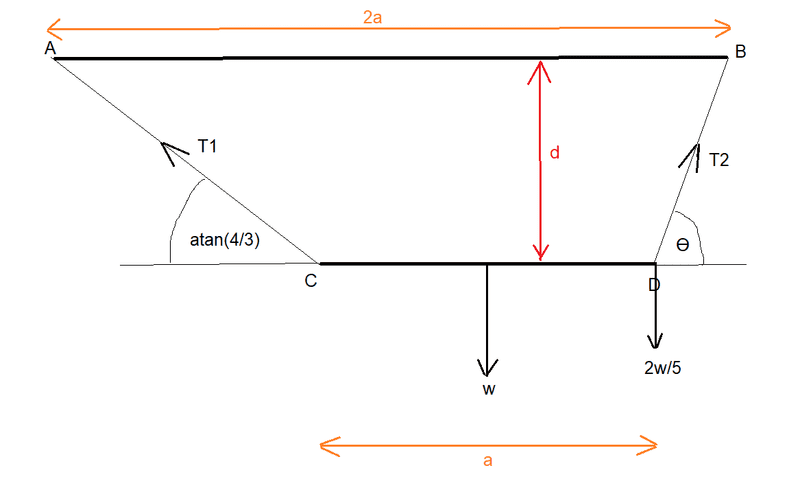I have found that T1 = 5W/8 and T2 = 39W/40 and that Ɵ = atan(12/5). This last answer agrees with the book answer. (This I did by equating forces horizontally, vertically and by taking moments about D and solving these equations for T1, T2 and Ɵ)

I have tried to involve d by taking moments about points on the line AB (for instance about the point on AB vertically above D) but this always leads to 1 = 1.

Thanks for any help in showing me how I can prove that d = (6/7)a.

Mitch.

 

[haruspex]

Homework Statement:: To find the distance of a horizontally suspended rod from a ceiling
Relevant Equations:: Moments and equating of forces

tried to involve d by taking moments

Having found those angles, there is no need for any further mechanical analysis; it's just geometry.
Take vertical lines through C, D to meet AB at E, F. In terms of d, how long are AE and BF?

 

[gnits]

Having found those angles, there is no need for any further mechanical analysis; it's just geometry.
Take vertical lines through C, D to meet AB at E, F. In terms of d, how long are AE and BF?

Thanks very much, Just wasn't seeing it. Much obliged.