phymath7
- 48
- 4
- Homework Statement
- In my physics lab experiment,I need to find out the critical damping resistance of a ballistic galvanometer (The associated circuit is given in the attempt section) by drawing ##\lambda## vs. ##R_2## graph where ##\lambda## is the logarithmic decrement of deflection of galvanometer .
- Relevant Equations
- $$\omega=\sqrt{\omega_0{}^2 -\frac{\gamma^2}{4}}$$
where ##\omega## is the damped angular frequency and ##\omega_0## is the undamped angular frequency
The differential equation of the motion of the galvanometer(wrt time):
$$\ddot \theta+\gamma\dot \theta +k^2\theta=0$$
Relation between ##\lambda## and ##\gamma ## is:
$$\lambda=\frac{\gamma T}{4}$$
Where
$$\gamma =\frac{\beta +\frac {a} {R_2 +G}}{I}$$
##\beta## and 'a' are constant,G is the galvanometer resistance and T is the time period.
At critical condition, ##\omega=0## so time period will be infinite and so will be ##\lambda##.Therefore, the critical resistance will be the corresponding resistance(plus galvanometer resistance)of the asymptote of ##\lambda## vs. ##R_2## graph(the graph is a rectangular hyperbola).
But here's where I'm stuck.How am I supposed to find the asymptote of the graph only having the observed data and not the explicit function?
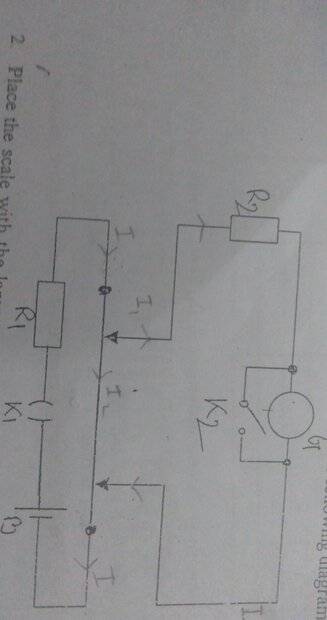
But here's where I'm stuck.How am I supposed to find the asymptote of the graph only having the observed data and not the explicit function?
Last edited: