arpon
- 234
- 16
Are the accelaration and forces in different inertial referance frame equal ?
The discussion centers on the differences in acceleration and forces across different inertial reference frames, particularly in the context of Special Relativity. It is established that coordinate acceleration changes with reference frames, while proper acceleration, treated as a 4-vector, remains invariant. The conversation highlights the importance of understanding vector quantities and their transformations, emphasizing that the concept of "relativistic mass" is outdated in modern physics. For a deeper understanding, the discussion references Wikipedia's article on mass in special relativity.
PREREQUISITESStudents and professionals in physics, particularly those studying relativity, as well as educators seeking to clarify concepts of acceleration and force in different inertial frames.
arpon said:Are the accelaration and forces in different inertial referance frame equal ?
The precise relativistic expression (which is equivalent to Lorentz's) relating force and acceleration for a particle with non-zero rest massmoving in the x direction with velocity v and associated Lorentz factor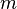 is
is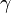
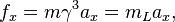
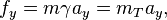
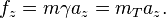
arpon said:Are the accelaration and forces in different inertial referance frame equal ?
Is there any straight forward way to prove these equations by using special relativity ?pervect said:I'm not sure where the best reference is, Wiki has some discussion of the issues at http://en.wikipedia.org/wiki/Mass_in_special_relativity#Transverse_and_longitudinal_mass
arpon said:Is there any straight forward way to prove these equations by using special relativity ?