physics kiddy
- 135
- 1
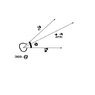
To add two vectors, a\rightarrow and b\rightarrow we use the formula \sqrt{}a2+b2+2abcosθ
where θ is the smallest angle between vectors a and b. Is there any way I can use the bigger angle to calculate the sum ? It's not a homework, just a question from my intution.
I have attached a pic also... Thanks in advance for help
where θ is the smallest angle between vectors a and b. Is there any way I can use the bigger angle to calculate the sum ? It's not a homework, just a question from my intution.
I have attached a pic also... Thanks in advance for help