- #1
Remle
- 12
- 8
- Homework Statement
- Two forces with magnitude of 15 pounds and 35 pounds and an angle of between them are applied to an object. Find magnitude of the resultant vector.
- Relevant Equations
- Law of cosine and law sine
Ok. My problem is what angle to choose when adding vector. Statement does not tell me which one is the "first" force vector. So, when using the law of sine formula I get two results.
First, using cosine to get the magnitude:
$$\vec c = \sqrt{a^2 + b^2 +2ab\cos\theta},$$
$$\vec c = \sqrt{15^2 + 35^2 +2(15(35) \cdot \cos(40)},$$
$$\vec c = 47~\text{lbs}$$
NOW; how and what angle do I choose for the resultant? (I know the problem is not asking for it but I want to practice). Picture of it attached.
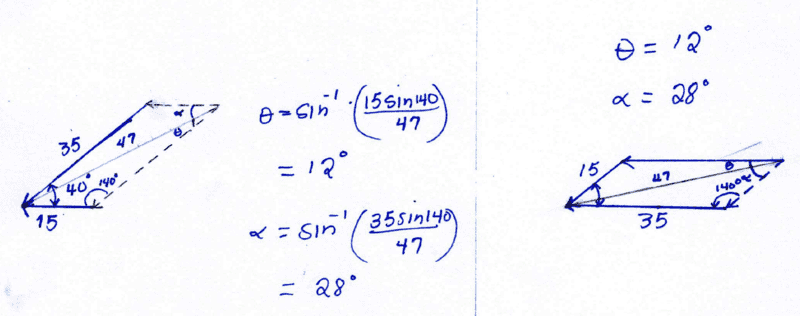
First, using cosine to get the magnitude:
$$\vec c = \sqrt{a^2 + b^2 +2ab\cos\theta},$$
$$\vec c = \sqrt{15^2 + 35^2 +2(15(35) \cdot \cos(40)},$$
$$\vec c = 47~\text{lbs}$$
NOW; how and what angle do I choose for the resultant? (I know the problem is not asking for it but I want to practice). Picture of it attached.
Last edited by a moderator: