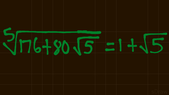SUMMARY
The discussion focuses on algebraically verifying the radical equation \(1+\sqrt{5}\) as a root of the quadratic equation \(x^2-2x-4=0\). The coefficients of the expansion \((1+\sqrt{5})^n\) are derived recursively using the relation \(A_{n}=2A_{n-1}+4A_{n-2}\), leading to the conclusion that \((1+\sqrt{5})^5=176+80\sqrt{5}\). Additionally, the binomial theorem is applied to confirm the identity \(176+80\sqrt{5}=(1+\sqrt{5})^5\), validating the original equation.
PREREQUISITES
- Understanding of quadratic equations, specifically \(x^2-2x-4=0\)
- Familiarity with recursive sequences and their applications
- Knowledge of the binomial theorem and its expansion
- Ability to manipulate algebraic expressions involving radicals
NEXT STEPS
- Study the derivation of recursive sequences in algebra
- Learn about the binomial theorem and its applications in polynomial expansions
- Explore methods for verifying identities in algebraic equations
- Investigate further examples of radical equations and their algebraic solutions
USEFUL FOR
Mathematicians, educators, and students interested in algebraic methods for solving radical equations and verifying identities without calculators.