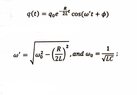Unraveling the Enigma: Understanding the Equation

[hidemi]

Homework Statement

An RLC circuit has a resistance of 200 Ω, an inductance of 15 mH, and a capacitance of 34nF. At time t = 0, the charge on the capacitor is 25
μC and there is no current flowing. After five complete cycles the energy stored in the capacitor is:

A) 0.64 μJ
B) 77 μJ
C) 0.49 mJ
D) 1.8 mJ
E) 9.2 mJ

The answer is A.

Relevant Equations

(see better expression below)

The equation is the only equation discussed in the textbook.
Is there a hint of how I could start this?

 

[Delta2]

Yes well, you should find the charge on the capacitor after five complete cycles. To find it you will use the first equation you give in the attached picture.

You can calculate $\omega'$ from the given values for R L C, and also $q_0$ and $\phi$ from the initial conditions of $q(0)=25\mu C,I(0)=0$.

Also once you find $\omega'$ find $T'=\frac{2\pi}{\omega'}$ which is the duration of one cycle. Finally put $t=5T'$ in the initial equation for $q(t)$ and find $q'=q(5T')$. The energy stored will be $$E=\frac{1}{2}\frac{q'^2}{C}$$.

 

[hidemi]

Thanks for the hint. I got it.