George Zucas
- 47
- 0
Hello,
I am trying to analyze a bolted connection. I don't remember anything about bolt connections, so I am studying at the same time ( the purpose is to actually study before actually designing a bolted connection). I designed the system itself and found the stresses on the connection and trying to understand whether the current bolt system is enough to support it.
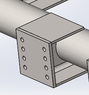
Here is the problem: The bolted connection has 8 M20 bolts, 4 at the left hand side and 4 at the right hand side, so not symmetrical. The connection is under all kinds of forces and bending moments, so Fx, Fy, Fz and Mx, My, and Mz are all present (x being the direction perpendicular to the cross section). The stresses due to bending moments are where I am stuck.
Here is what I did so far:
I assumed only the four bolts at the corners are carrying the loads so that the arrangement becomes symmetrical for simplicity. For example, the bending moment in the y direction is 7500000 Nmm. I carried this bending moment to the centroid. The distance between a bolt and the centroid is about 150 mm. So the summation of moments on each bolt should be equal to the actual bending moment. Is that a correct procedure (this is what I get from the textbook)?
7500000/4=1875000 Nmm (4 bolts assumed)
1875000/150=12500 N (Force causing the bending moment)
12500N/245=51 MPa tensile stress (245 mm being the tensile stress area of a M20 bolt).
Similarly in z direction (11200000 Nmm),
112000000/4=2800000 Nmm
2800000/150=18667 N
18667/245=76 MPa tensile stress
And how should I proceed in the x direction? This method wouldn't work and I haven't come up with something yet.
Thanks for any help.
I am trying to analyze a bolted connection. I don't remember anything about bolt connections, so I am studying at the same time ( the purpose is to actually study before actually designing a bolted connection). I designed the system itself and found the stresses on the connection and trying to understand whether the current bolt system is enough to support it.
Here is the problem: The bolted connection has 8 M20 bolts, 4 at the left hand side and 4 at the right hand side, so not symmetrical. The connection is under all kinds of forces and bending moments, so Fx, Fy, Fz and Mx, My, and Mz are all present (x being the direction perpendicular to the cross section). The stresses due to bending moments are where I am stuck.
Here is what I did so far:
I assumed only the four bolts at the corners are carrying the loads so that the arrangement becomes symmetrical for simplicity. For example, the bending moment in the y direction is 7500000 Nmm. I carried this bending moment to the centroid. The distance between a bolt and the centroid is about 150 mm. So the summation of moments on each bolt should be equal to the actual bending moment. Is that a correct procedure (this is what I get from the textbook)?
7500000/4=1875000 Nmm (4 bolts assumed)
1875000/150=12500 N (Force causing the bending moment)
12500N/245=51 MPa tensile stress (245 mm being the tensile stress area of a M20 bolt).
Similarly in z direction (11200000 Nmm),
112000000/4=2800000 Nmm
2800000/150=18667 N
18667/245=76 MPa tensile stress
And how should I proceed in the x direction? This method wouldn't work and I haven't come up with something yet.
Thanks for any help.
Last edited: