evinda
Gold Member
MHB
- 3,741
- 0
Hello! (Wave)
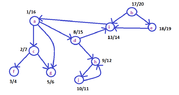
I want to apply the Depth-first search algorithm at the following graph.
We consider that at the iteration of the algorithm, we look at the nodes alphabetically. Also the nodes are registered alphabetically in each list. I want to calculate the "discovery" time and the "finish" time for each node and also the kind of each edge.
View attachment 3654
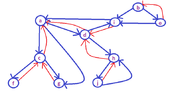
I found these "discovery" and "finish" times:
View attachment 3655
Have I calculated them right? (Thinking)
Also, in order to find the kind of the edges I wanted to use this:
$$\begin{bmatrix}
\text{ tree edges: } x \to y & [d[y],f[y]] \subset [d[x],f[x]] \\ \\
\text{forward edges: } x \to y & [d[x],f[x]] \subset [d[y],f[y]] \\ \\
\text{back edges: } x \to y & [d[y],f[y]] \subset [d[x],f[x]] \\ \\
\text{Cross edges: } x \to y & [d[x],f[x]] \cap [d[y],f[y]]=\varnothing
\end{bmatrix}$$
But, when we have for example the case $[d[y],f[y]] \subset [d[x],f[x]]$ how can we know if it is a tree edge or a back edge? (Thinking)
I want to apply the Depth-first search algorithm at the following graph.
We consider that at the iteration of the algorithm, we look at the nodes alphabetically. Also the nodes are registered alphabetically in each list. I want to calculate the "discovery" time and the "finish" time for each node and also the kind of each edge.
View attachment 3654
Code:
Depthfirstsearch(G)
for each v ∈ V
color[v]=white
p[v]=NIL
time=0
for each v ∈ V
if color[v]=white then
Visit(v)
Code:
Visit(u)
color[u]=gray
time=time+1
d[u]=time
for each v ∈ Adj[u]
if color[v]=white then
p[v]=u
Visit(v)
color[u]=black
time=time+1
f[u]=timeI found these "discovery" and "finish" times:
View attachment 3655
Have I calculated them right? (Thinking)
Also, in order to find the kind of the edges I wanted to use this:
$$\begin{bmatrix}
\text{ tree edges: } x \to y & [d[y],f[y]] \subset [d[x],f[x]] \\ \\
\text{forward edges: } x \to y & [d[x],f[x]] \subset [d[y],f[y]] \\ \\
\text{back edges: } x \to y & [d[y],f[y]] \subset [d[x],f[x]] \\ \\
\text{Cross edges: } x \to y & [d[x],f[x]] \cap [d[y],f[y]]=\varnothing
\end{bmatrix}$$
But, when we have for example the case $[d[y],f[y]] \subset [d[x],f[x]]$ how can we know if it is a tree edge or a back edge? (Thinking)