jdang
- 3
- 0
Homework Statement
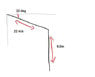
- a ball rolls off an incline on top of a 9.0m building
- at a velocity of 22m/s
- 32° below the horizontal
- how far from the base of the building will the ball hit the ground?
- [ANS = 11m)
Homework Equations
- vf^2 = vi^2 + 2ad
- d = ((vf+vi)/2)t
- d = vt
The Attempt at a Solution
- x (um)
- v = 22cos32 = 18.657...m/s
- y (uam)
- a = -9.81m/s^2
- vi = -22sin32 = -11.658...m/s
- d = 9.0m
- vf^2 = vi^2 + 2ad
vf^2 = 312.494...m^2/s^2
vf = 17.677...m/s
- d = ((vf+vi)/2)t
-9.0m = ((17.677...m/s - 11.658...m/s)/2)t
t = ((17.677...m/s - 11.658...m/s)/2) / 9.0m
t = 0.334...s
- d = vt
d = 6.495...m
d = 6.5m
I'm not sure where I made my mistake since I am about 4.5m off.
Attachments
Last edited: