Homework Help Overview
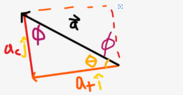
The discussion revolves around the calculation of an angle related to acceleration in non-uniform circular motion. Participants are examining the relationship between radial and tangential accelerations and how these contribute to the total acceleration vector.
Discussion Character
- Conceptual clarification, Assumption checking, Mathematical reasoning
Approaches and Questions Raised
- Participants are questioning the use of different ratios in the tangent function for calculating the angle. There is discussion about the notation used for inverse trigonometric functions and the interpretation of symbols in the context of degrees.
Discussion Status
There is an ongoing exploration of the relationships between different types of acceleration and how they relate to the angle being calculated. Some participants are clarifying misunderstandings about notation and the geometric interpretation of the problem, while others are drawing diagrams to visualize the situation.
Contextual Notes
Participants note that the angle is defined as the one between the radial acceleration and the total acceleration, and there is mention of a specific angle being measured in a particular way relative to a cord in the diagram. There is also acknowledgment of the potential confusion arising from changing symbols during problem-solving.