MHB Angles in congruence triangles

  • Thread starter Thread starter sts1983
  • Start date Start date
  • Tags Tags
    Angles Triangles
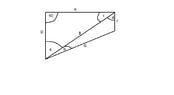
AI Thread Summary
The discussion centers on solving for angles and sides in congruent triangles given certain known values. The user seeks to determine the values of b, d, G, and F, with the constraint that c + d equals 90 degrees. A response highlights the uncertainty in finding F due to a lack of constraints that would limit its length while keeping other values constant. Additionally, there is a request for clarification on which congruent triangles are being referenced. The conversation emphasizes the need for more information to solve the problem effectively.
sts1983
Messages
1
Reaction score
0
View attachment 8476

I am trying to work out the above problem.
Known are: D,A,B,a,c,d. I need to work out b,d,G and F. Any ideas?

c+d = 90 degrees.

Regards,

Stan
 

Attachments

  • trianles.jpg
    trianles.jpg
    26.7 KB · Views: 133
Mathematics news on Phys.org
Hi, and welcome to the forum!

A am not sure we can find F because I don't see any constraint that prevents one from making F longer while preserving D, A, B, a, c, and d.

Also, what congruent triangles do you mean in the thread title?
 

Thread 'Trigonometry problem of interest'

Seemingly by some mathematical coincidence, a hexagon of sides 2,2,7,7, 11, and 11 can be inscribed in a circle of radius 7. The other day I saw a math problem on line, which they said came from a Polish Olympiad, where you compute the length x of the 3rd side which is the same as the radius, so that the sides of length 2,x, and 11 are inscribed on the arc of a semi-circle. The law of cosines applied twice gives the answer for x of exactly 7, but the arithmetic is so complex that the...
View full post »
Thread 'Imaginary Pythagoras'

Thread 'Imaginary Pythagoras'

I posted this in the Lame Math thread, but it's got me thinking. Is there any validity to this? Or is it really just a mathematical trick? Naively, I see that i2 + plus 12 does equal zero2. But does this have a meaning? I know one can treat the imaginary number line as just another axis like the reals, but does that mean this does represent a triangle in the complex plane with a hypotenuse of length zero? Ibix offered a rendering of the diagram using what I assume is matrix* notation...
View full post »

Thread 'Fermat's Last Theorem'

Fermat's Last Theorem has long been one of the most famous mathematical problems, and is now one of the most famous theorems. It simply states that the equation $$ a^n+b^n=c^n $$ has no solutions with positive integers if ##n>2.## It was named after Pierre de Fermat (1607-1665). The problem itself stems from the book Arithmetica by Diophantus of Alexandria. It gained popularity because Fermat noted in his copy "Cubum autem in duos cubos, aut quadratoquadratum in duos quadratoquadratos, et...
View full post »

Similar threads

MHB Difference of angles in a triangle
Replies
4
Views
2K
MHB Can an Ellipse Help Solve the Scalene Triangle Problem?
Replies
1
Views
1K
I Given a triangle ABC, on which side of the triangle does the point D lie?
Replies
6
Views
2K
MHB Find Length of Side in Right Triangle w/ 45°, 90°, and 45° Angle
Replies
2
Views
2K
MHB Proving Equality of Angles in an Acute Triangle
Replies
4
Views
1K
B In a triangle, is the angle between the points of contact of the inscribed circle with the sides 120 degrees?
Replies
2
Views
922
MHB Act.ge.5 third angle of triangle
Replies
1
Views
1K
MHB Can You Find the Angle in This Isosceles Triangle Problem?
Replies
1
Views
1K
I Chiral symmetries in E[SUP]^n[/SUP]
Replies
1
Views
2K
B Understanding the Pythagorean Theorem
Replies
38
Views
4K

Hot Threads

Recent Insights

Back
Top