tristancohn
- 2
- 0
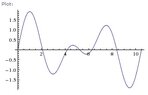
i have a waveform:
y2(x)= sin(x*1.2)+sin(x*1.8)
the first 6 nodes, meaning the parts of the wave where y2=0 come up on my graph at around x =
2.094
4.189
5.236
6.283
8.377
10.471
you can find the nodes easily (where y2=0) with either x = n*pi/(1.5) or x = (2n+1)*(pi/0.6), where n = 0, 1,2 3, and so on.
what I really want to find is the antinodes (peaks) of y2, similar to on this graph where the line turns black:
http://upload.wikimedia.org/wikipedia/commons/7/7a/Graph_of_sliding_derivative_line.gif
which are at around x =
1.006
2.979
4.665
5.808
7.492
9.466
I know that the antinodes for y2 come up at 1.8*COS(1.8*x)+1.2*COS(1.2*x)=0
but i just can't find a clean way of finding them.

y2(x)= sin(x*1.2)+sin(x*1.8)
the first 6 nodes, meaning the parts of the wave where y2=0 come up on my graph at around x =
2.094
4.189
5.236
6.283
8.377
10.471
you can find the nodes easily (where y2=0) with either x = n*pi/(1.5) or x = (2n+1)*(pi/0.6), where n = 0, 1,2 3, and so on.
what I really want to find is the antinodes (peaks) of y2, similar to on this graph where the line turns black:
http://upload.wikimedia.org/wikipedia/commons/7/7a/Graph_of_sliding_derivative_line.gif
which are at around x =
1.006
2.979
4.665
5.808
7.492
9.466
I know that the antinodes for y2 come up at 1.8*COS(1.8*x)+1.2*COS(1.2*x)=0
but i just can't find a clean way of finding them.