Approximation for volatility of random variable

[Petr Rygr]

Hello, could anyone please explain me some logic or derivation behind the approximation:

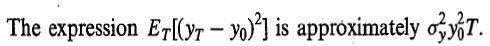
Found it in the Hull Derivatives book without further explanation. Thanks for help

 

[EnumaElish]

See (3) and the related text in http://econwpa.repec.org/eps/fin/papers/0212/0212005.pdf