- #1
fog37
- 1,568
- 108
- TL;DR Summary
- Understand the correct relation between random variable and events...
Hello,
I am solid on the following concepts but less certain on the correct understanding of what a random variable is...
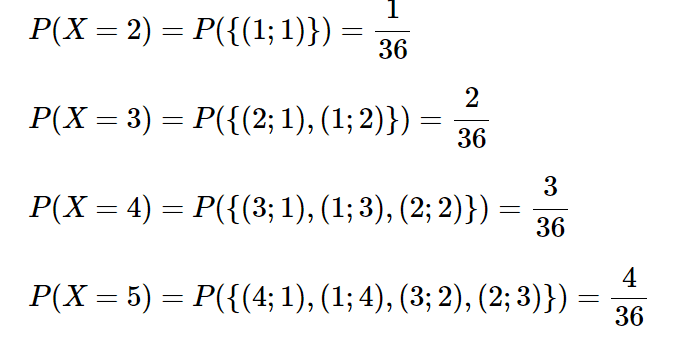
##X## labels the elementary event ##{(1;1)}## as ##2##
##X## labels the composite event ##{(2;1), (1;2)}## as ##3##
##X## labels the composite event ##{(3;1), (1;3), (2;2)}## as ##4##
The rule behind the random variable ##X## is really to assign a number to events whose outcomes have something in common, in this case their sum being the same number...That sounds convoluted...
Thank you for any clarification.
I am solid on the following concepts but less certain on the correct understanding of what a random variable is...
- Random Experiment: an experiment that has an uncertain outcome.
- Trials: how many times we sequentially repeat a random experiment.
- Sample space ##S##: the set of ALL possible individual outcomes of a random experiment. When we perform the experiment, we may know which outcomes may happen but don't know with certainty which one of those outcomes will happen.
- Event ##E##: an event ##E## is either a single outcome (called elementary event) or a collection of outcomes from the sample space ( called composite event, i.e. a subset of sample space ##S##).
- When an event happens/occurs, it means that just one of the outcomes in the set ##E## has occurred/materialized.
- Probability: a real-valued function that associates a real number between 0 and 1 to an event ##E##. So different events may have different probabilities. The higher the number the more likely it is for that event ##E## to occur. So probability is a function that associates real numbers to different events.
- Random variable r.v. : also a real-valued function. I would say that it also associates a real number to different events....Is that correct?
- Random experiment: throwing two fair dies.
- Number of Trials: 1
- Sample space ##S={(1;1) , (2;1) , (3;1) , ..., (6;6)} ##.
- Number of outcomes: 36
- Random variable ##X##: "the sum of the faces, face i and face j, of the two dies" . Is this statement really representing the rule ##X: i+j##? Or is a random variable ##X## a real-value function whose input is a set of particular events ##E##? A random variable clearly associates a number to different events. But also the probability function associates a number, the probability value, to different events. Is a random variable simply a function that "relabels" particular events?
##X## labels the elementary event ##{(1;1)}## as ##2##
##X## labels the composite event ##{(2;1), (1;2)}## as ##3##
##X## labels the composite event ##{(3;1), (1;3), (2;2)}## as ##4##
The rule behind the random variable ##X## is really to assign a number to events whose outcomes have something in common, in this case their sum being the same number...That sounds convoluted...
Thank you for any clarification.