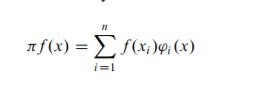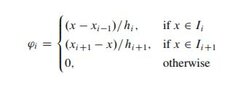evinda
Gold Member
MHB
- 3,741
- 0
Hello! (Wave)
I want to prove that each continuous function $f$ in a closed and bounded interval $[a,b]$ can be approximated uniformly with polynomials, as good as we want, i.e. for a given positive $\epsilon$, there is a polynomial $p$ such that
$$\max_{a \leq x \leq b} |f(x)-p(x)|< \epsilon.$$
Firstly, we should make sure that we can assume without loss of generality that the interval $[a,b]$ is contained in the open interval $(-\pi,\pi)$.
But why can we assume this? (Thinking)
I want to prove that each continuous function $f$ in a closed and bounded interval $[a,b]$ can be approximated uniformly with polynomials, as good as we want, i.e. for a given positive $\epsilon$, there is a polynomial $p$ such that
$$\max_{a \leq x \leq b} |f(x)-p(x)|< \epsilon.$$
Firstly, we should make sure that we can assume without loss of generality that the interval $[a,b]$ is contained in the open interval $(-\pi,\pi)$.
But why can we assume this? (Thinking)