Johncena said:
I have been stuck on this problem for 8 hours. Can anyone please help me? it would be great if full solution is provided, but even a general overview would help.
PQRS is a rectangle with PQ=20 and QR=5. Point X lies on the line PQ and Y on RS such that angle PYQ is 90 degrees. Angle SXR is also 90. Triangle PYQ is congruent to triangle SXR.
Let the point of intersection of PY and SX be D and intersection of QY and XR be E.
Find the area of DYEX.
Hi Johncena! Welcome to MHB, and thanks for posing this interesting problem.
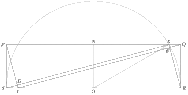
Let $N$ be the midpoint of $PQ$, and $O$ the midpoint of $RS$. A circle with $RS$ as diameter (so centred at $O$, and with radius $10$) will cut $PQ$ at the point $X$ (because the right angle $SXR$ is an angle in a semicircle). As far as I can see, $X$ can be either of the points where the circle crosses $PQ$, so it could equally well be at the point vertically above $Y$. In that case, the region $DYEX$ would be kite-shaped. Maybe that is what you wanted? But I am assuming, as did
Prove It, that $X$ is chosen so that $PX=YR$. In that case, $DYEX$ will be a long, very narrow, rectangle, as in the above diagram.
By Pythagoras in the triangle $ONX$, $NX^2 = OX^2 - ON^2 = 100 - 25 = 75$. Therefore $OY = NX = \sqrt{75} = 5\sqrt3.$ Hence $SY = SO - OY = 5(2-\sqrt3).$
By Pythagoras again, in the triangle $PSY$, $PY^2 = PS^2 + SY^2 = 25 + 25\bigl(2-\sqrt3\bigr)^2 = 100\bigl(2-\sqrt3\bigr) = 20\cdot SY.$ Therefore $\Bigl(\dfrac{SY}{PY}\Bigr)^2 = \dfrac{SY}{20}.$
The triangles $PSY$ and $SDY$ are similar, having equal angles. The ratio of their areas is the square of the ratio of their sides. Therefore the area of the little triangle $SDY$ is given by $$\operatorname{area}(SDY) = \Bigl(\dfrac{SY}{PY}\Bigr)^2 \!\operatorname{area}(PSY) = \dfrac{SY}{20}\cdot \frac12 PS\cdot SY = \dfrac{SY}{20}\cdot\dfrac{5SY}2 = \dfrac{SY^2}8 = \dfrac{25}8\bigl(2-\sqrt3\bigr)^2 = \dfrac{25}8\bigl(7 - 4\sqrt3\bigr).$$
Next, the area of the parallelogram $PXRY$ is (base)$\times$(vertical height) $= (RO+OY)\times5 = 5\bigl(10 + 5\sqrt3\bigr) = 25\bigl(2 + \sqrt3\bigr).$
The two triangles $PYQ$ and $SXR$ together cover the whole of the parallelogram $PXRY$, but they overlap over the rectangle $DYEX$ and they also include the two (equal) little triangles $SDY$ and $QEX.$ Therefore $$\operatorname{area}(PYQ) + \operatorname{area}(SXR) = \operatorname{area}(PXRY) + \operatorname{area}(DYEX) + 2\operatorname{area}(SDY),$$ and so $$\begin{aligned} \operatorname{area}(DYEX) &= \operatorname{area}(PYQ) + \operatorname{area}(SXR) - \operatorname{area}(PXRY) - 2\operatorname{area}(SDY) \\ &= 50 + 50 - 25\bigl(2 + \sqrt3\bigr) - \dfrac{25}4\bigl(7 - 4\sqrt3\bigr) = \dfrac{25}4. \end{aligned}$$